Предмет: Алгебра,
автор: kamchibekovsanjar06
Помогите пожалуйста
Приложения:
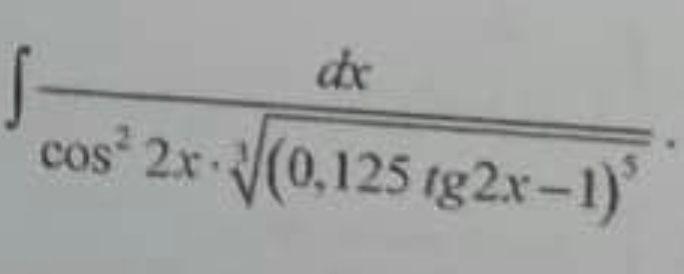
Ответы
Автор ответа:
1
Решение.
Применяем метод замены переменной . Обозначаем подкоренное выражение новой переменной t .
Похожие вопросы
Предмет: Математика,
автор: Dopomoga12345
Предмет: Биология,
автор: onaigali7963
Предмет: Математика,
автор: turdaliyevislam316
Предмет: Математика,
автор: jpashko
Предмет: Английский язык,
автор: nurjigit1308