Question

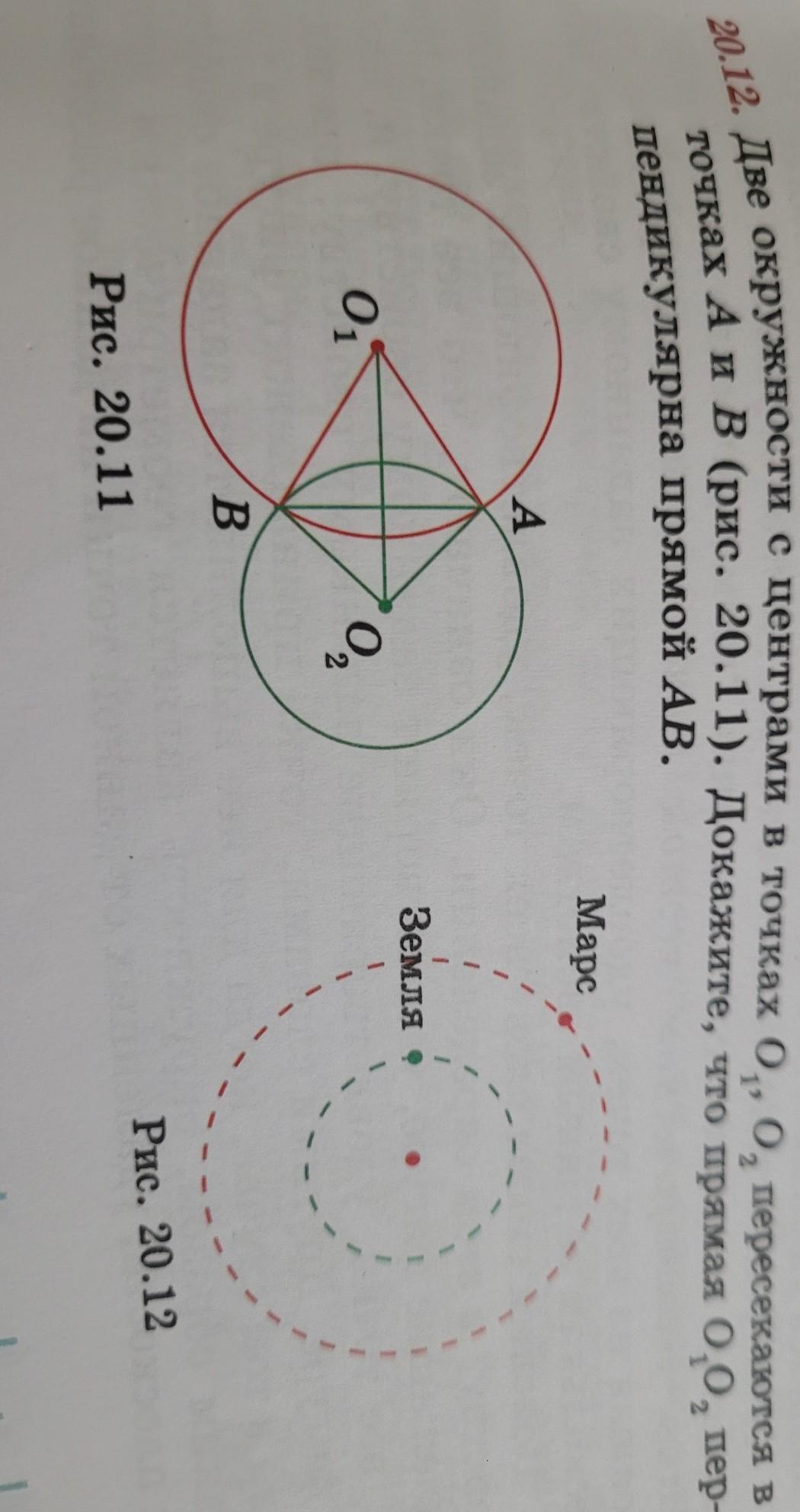
20.12. Две окружности с центрами в точках О., 0, пересекаются в точках А и В (рис. 20.11). Докажите, что прямая 0,0, пер- пендикулярна прямой АВ. 01 A в Рис. 20.11 Рис. 20.10 Ог Марс Земля Рис. 20.12 117 B reauempus​

Answer 1

Ответ:

Доказали, что O₁O₂⊥АВ

Объяснение:

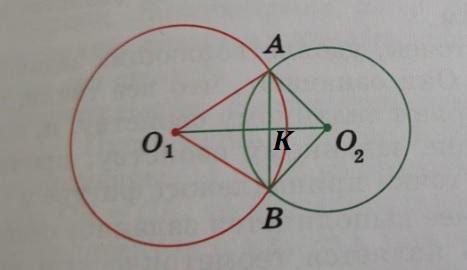
Две окружности с центрами в точках О₁, O₂, пересекаются в точках А и В. Докажите, что прямая O₁O₂ перпендикулярна прямой АВ.

1. Рассмотрим ΔО₁АО₂ и ΔО₁ВО₂.

У них:

• О₁А=О₁В - как радиусы окружности с центром в точке О₁

• О₂А=О₂В - как радиусы окружности с центром в точке О₂

• О₁О₂ - общая

ΔО₁АО₂ = ΔО₁ВО₂ - по трём сторонам ( 3 признак равенства треугольников)

Следовательно ∠АО₁О₂=∠ВО₁О₂, ∠АО₂О₁=∠ВО₂О₁.

2. В ΔАО₁В:  О₁А=О₁В, следовательно  ΔАО₁В - равнобедренный.

Так как ∠АО₁О₂=∠ВО₁О₂, то О₁К- биссектриса ΔАО₁В.

В равнобедренном треугольнике биссектриса  является также высотой, следовательно О₁К⊥АВ.

Таким образом O₁O₂⊥АВ, что и требовалось доказать.

#SPJ1