Question

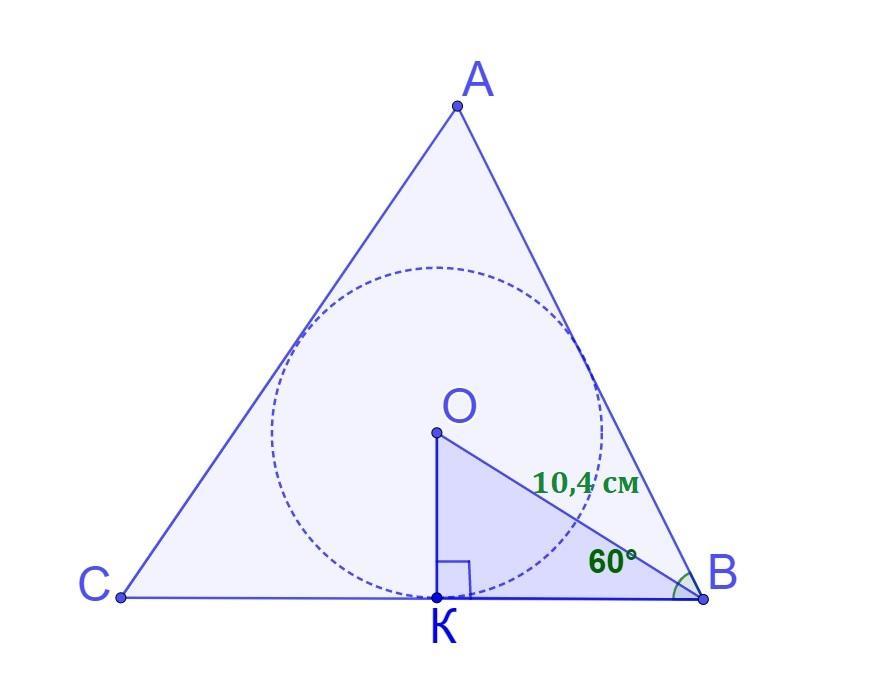
У трикутнику АВС кут В =60 градусів. Відстань від центра вписаного у трикутник кола до вершини В дорівнює 10,4 см. Знайдіть радіус цього кола.

Answer 1

Ответ:

Радіус кола дорівнює 5,2 см

Объяснение:

У трикутнику АВС кут В =60°. Відстань від центра вписаного у трикутник кола до вершини В дорівнює 10,4 см. Знайдіть радіус цього кола.

• Центр вписаного в трикутник кола лежить в точці перетину бісектрис ціого трикутника
• Катет прямокутного трикутника, що лежить навпроти кута 30°, дорівнює половині гіпотенузи.

Роз'вязання

1) Нехай ΔАВС - даний трикутник. ∠В=60°. Точка О - центр вписаного кола - знаходиться у точці перетину бісектрис.

Отже ВО - бісектриса ∠В. Тому:

∠ОВК=∠ОВА=∠В:2=30° - за властивістю бісектриси кута трикутника.

2) ОК- радіус кола, вписаного в ΔАВС. К - точка дотику зі стороною ВС  ⇒ ОК⊥ВС

3) В прямокутному трикутнику ОКВ (∠ОКВ=90°) катет ОК лежить навпроти кута ∠ОВК=30°, тому він дорівнює половині гіпотенузи ВО.

ВО=10,4 см - за умовою. Тому:

ОК=ВО:2=10,4:2=5,2 (см)

Відповідь: 5,2 см

#SPJ1