Помогите, дам корону
Вирішить 3 системи лінійних рівняннь способом додавання
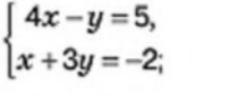
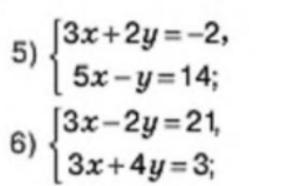
Ответы
Ответ:
первое:
4x - y = 5
x + 3y = -2
Спочатку ми можемо помножити друге рівняння на 4, щоб отримати коефіцієнт 4 перед x, як у першому рівнянні:
4x - y = 5
4x + 12y = -8
Тепер ми можемо відняти перше рівняння від другого, щоб усунути змінну x:
(4x + 12y) - (4x - y) = -8 - 5
Це дає нам:
13y = -13
Тепер ми можемо розв'язати це рівняння для y:
y = -1
Підставляючи це значення y в одне з оригінальних рівнянь, ми можемо знайти x:
4x - (-1) = 5
4x + 1 = 5
4x = 4
x = 1
Таким чином, розв'язок системи рівнянь методом додавання є (x, y) = (1, -1).
второе:
3x + 2y = -2 (1)
5x - y = 14 (2)
Можна помножити друге рівняння на 2, щоб отримати -2y у другому рівнянні, та додати його до першого рівняння, щоб отримати рівняння з однією змінною:
3x + 2y = -2 (1)
10x - 2y = 28 (3)
Потім можна додати рівняння (1) та (3), щоб усунути змінну y та знайти значення x:
13x = 26
x = 2
Після знаходження x можна підставити його у одне з рівнянь, наприклад у (2), щоб знайти значення y:
5x - y = 14
5(2) - y = 14
y = -6
Таким чином, розв'язок системи лінійних рівнянь методом додавання є (x,y) = (2,-6)
третья:
3x - 2y = 21 (1)
3x + 4y = 3 (2)
Можна помножити перше рівняння на 2, щоб отримати -4y у першому рівнянні, та додати його до другого рівняння, щоб отримати рівняння з однією змінною:
6x - 4y = 42 (3)
3x + 4y = 3 (2)
Потім можна додати рівняння (2) та (3), щоб усунути змінну y та знайти значення x:
9x = 45
x = 5
Після знаходження x можна підставити його у одне з рівнянь, наприклад у (1), щоб знайти значення y:
3x - 2y = 21
3(5) - 2y = 21
y = -3
Таким чином, розв'язок системи лінійних рівнянь методом додавання є (x,y) = (5,-3).