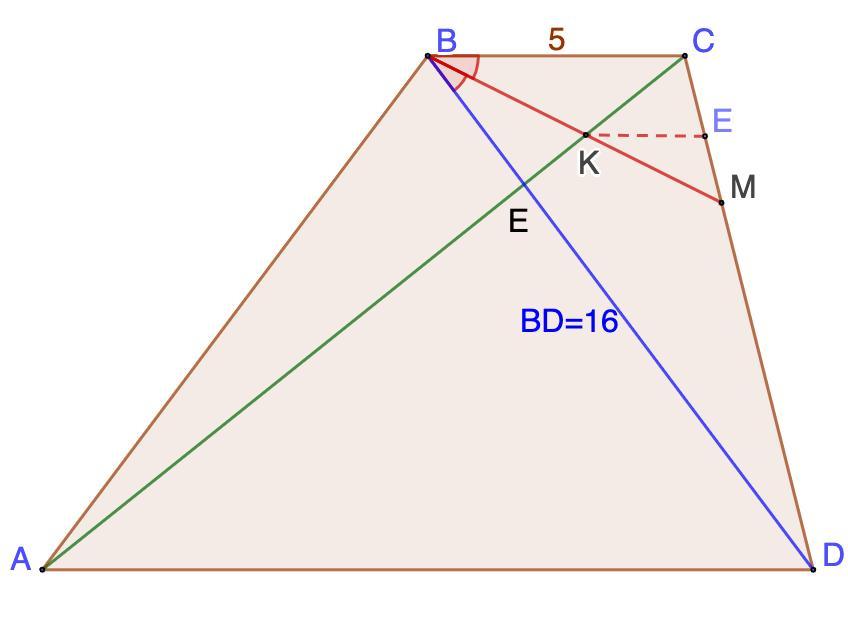
В трапеции ABCD меньшее основание BC равно 5, а диагональ BD равна 16. Биссектриса угла CBD пересекает диагональ AC в точке K такой, что CK:AK=1:6. Найдите длину основания AD.
Помогите, пожалуйстааааа!!
Ответы
Ответ:
Длина основания AD равна 14 ед.
Объяснение:
В трапеции ABCD меньшее основание BC равно 5, а диагональ BD равна 16. Биссектриса угла CBD пересекает диагональ AC в точке K такой, что CK:AK=1:6. Найдите длину основания AD.
Дано: ABCD - трапеция;
ВС = 5; BD = 16;
ВМ - биссектриса ∠CBD;
BM ∩ AC = K; CK : AK = 1 : 6;
Найти: AD
Решение:
Проведем ЕК || ВС.
1. CK : AK = 1 : 6 ⇒ СК : СА = 1 : 7
2. Рассмотрим ΔDBC
BM - биссектриса.
- Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон.
⇒ МС : МD = СВ : BD = 5 : 16
Пусть МС = 5х, тогда МК = 16х, а СD = 21x.
3. Рассмотрим ∠ACD.
КЕ || AD (построение)
- Если на одной стороне отложить отрезки и через их концы провести параллельные прямые, пересекающие другую сторону, то на другой стороне угла отложатся отрезки, пропорциональные данным.
⇒ СЕ : ED = CK : KA = 1 : 6
или СЕ : СD = 1 : 7
4. Рассмотрим ΔКЕМ и ΔВСМ.
КЕ || ВС (построение)
- Если две стороны треугольника пересекает прямая, параллельная третьей стороне, то она отсекает треугольник, подобный данному.
⇒ ΔКЕМ ~ ΔВСМ.
MC = 5x; ME = MC - CE = 5x - 3x = 2x.
Запишем отношения сходственных сторон:
5. Рассмотрим ΔКСЕ и ΔACD.
KE || AD
⇒ ΔКСЕ ~ ΔACD
Запишем отношения сходственных сторон:
Длина основания AD равна 14 ед.
#SPJ1
Ответ: Длина основания AD = 14 (ед)
Объяснение:
Обозначим AK = 6x , а EK = w ⇒ AE = 6x -w , также пусть BE = z ⇒
ED = 16 - z
Рассмотрим ΔBCD , поскольку биссектриса BF делит его противоположную сторону на два отрезка, длины которых пропорциональны соответствующим прилежащим сторонам треугольника ⇒
Теперь на этом же Δ-ке , применяем теорему Менелая , начиная со стороны BE
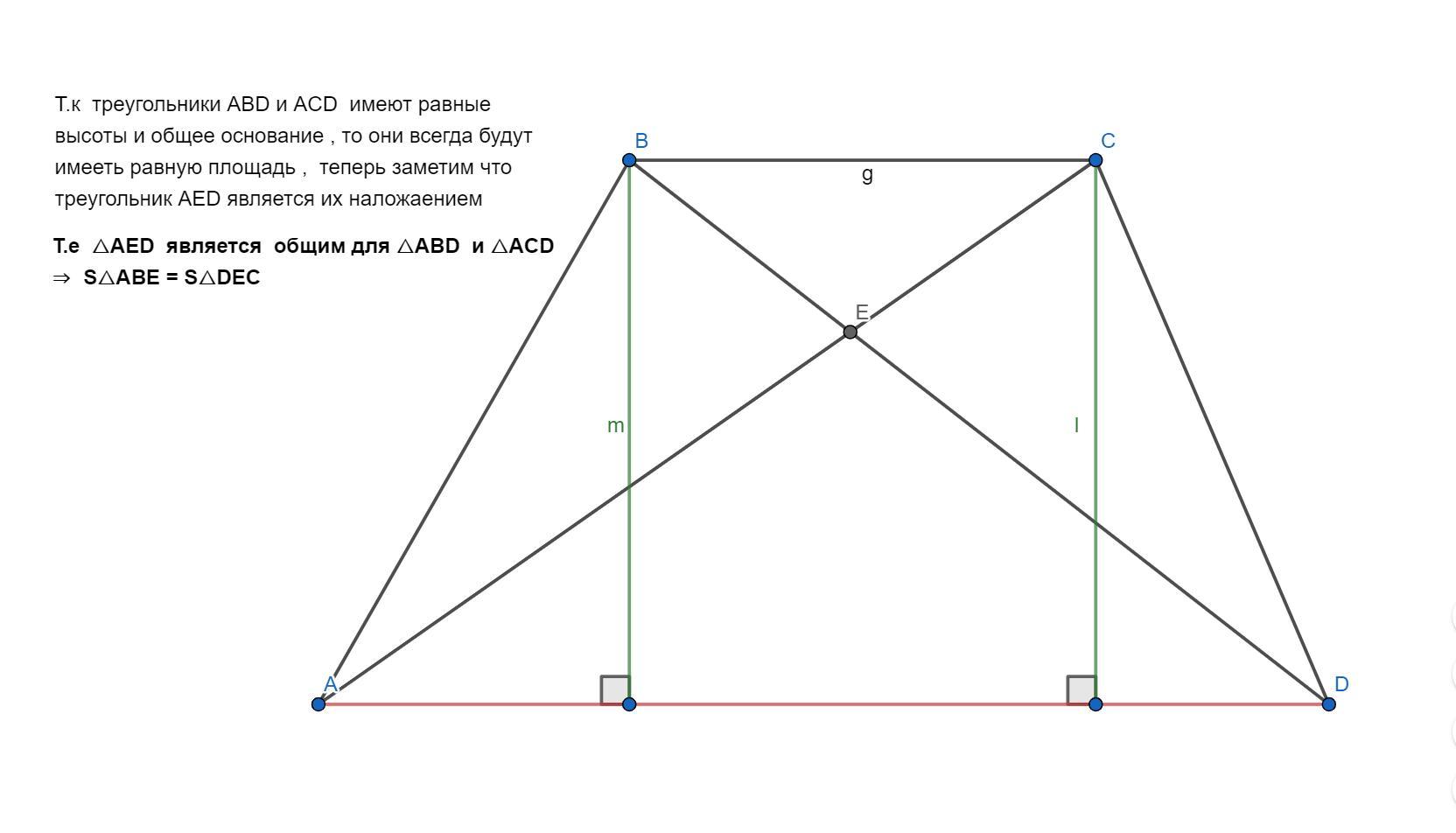
Поскольку нам дана трапеция , то треугольники ABE и DEC имеют равную площадь , и т.к ∠BEA = ∠ CEA как вертикальные
Тогда По формуле
Подставим xz = 5w
7·5w = 16w + 16x
35w = 16w + 16x
19w = 16x
То что мы вывели подставим в xz = 5w
В силу того , что BC ║ AD , диагонали BD и AC будут отсекать два подобных треугольника ΔBEC ≅ ΔAED
∠EAD = ∠ECB и ∠CBE = ∠EDA как соответственные углы
⇒ по свойству подобия :
#SPJ1