Дано:
BC=2см
АД=18см
S-?
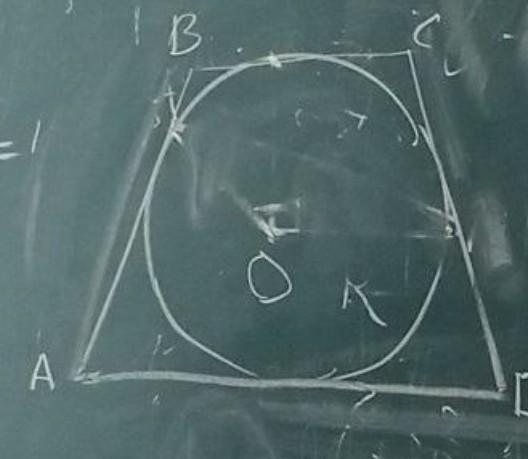
Ответы
Ответ:
Окрудность можно вписать в трапецию,если Сумма длин оснований равна сумме длин боковых сторон
ВС+АD=AB+CD
2+18=AB+CD
20=20
Ксли в трапецию вписана трапеция,то она равнобедренная
АВ=СD=20:2=10 см
Из точек В и С на БОльшее основание опустим высОты ВА1 и СD1-это перпендикуляры,которые отсекли от трапеции два равных прямоугольных треугольника,у которых гипотенуща-боковая сторона трапеции,равная 10 см,и катет,который вычислим таким образом
DD1=AA1=(AD-BC):2=(18-2):2=8 см
По теореме Пифагора узнаём величину высоты трапеции,в данном конкретном случае-это неизвестный катет прямоугольного треугольника
СD1=10^2-8^2=100-64=36
Корень квадратный из 36 равен 6
Высота равна 6 см
Площадь трапеции равна произведению полусуммы оснований на высоту
S=(BC+AD):2•CD1=(2+18):2•6=60 см^2
Объяснение: