Question

БУДЬ ЛАСКА З ПОВНИМ РІШЕННЯМ

Answer 1

Ответ:

Радіус меньшого кола дорівнює 4 см

Объяснение:

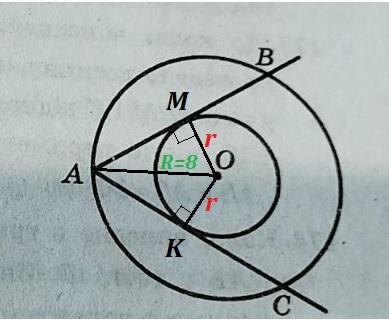
На рісунку два кола мають спільний центр О. Через точку А більшого кола проведено дотичні АВ і АС до меньшого кола. Знайдіть радіус меньшого кола, якщо радіус більшого дорівнює 8 см, а ∠ВАС=60°.

• Дотична до кола перпендикулярна радіусу, проведеному до точки дотику

• Якщо гіпотенуза і катет одного прямокутного трикутника дорівнюють відповідно гіпотенузі й катету другого, то такі трикутники рівні.

• В прямокутному трикутнику катет, що лежить проти кута 30 градусів дорівнює половині гіпотенузи.

Розв'язання:

За умовою дани два кола з спільним центром у точці О.

АО=R=8 см - радіус більшого кола.  

АВ І АС - дотичні до меншого кола. ∠ВАС=60°.

Проведем радіус ОМ в точку дотику М, та радіус ОК в точку дотику К.

За властивість дотичной до кола: ОМ⊥АВ, ОК⊥АС.

Розглянемо прямокутні трикутники АМО (∠АМО=90°) і АКО(∠АКО=90°)

• ОМ=ОК=r - як радіуси меньшого кола
• АО - спільна

ΔАМО=ΔАКО за гіпотенузою і катетом.

∠МАО=∠КАО - як відповідні кути рівних трикутників.

∠МАО=∠КАО=∠ВАС:2=60°:2=30°

У прямокутному трикутнику АМО катет МО лежить проти кута ∠МАО=30°, тому за властивістю він дорівнює  половині гіпотенузі АО:

r=МО=АО:2=8:2=4(см)