даю 30 балов нужно только 1 и 2
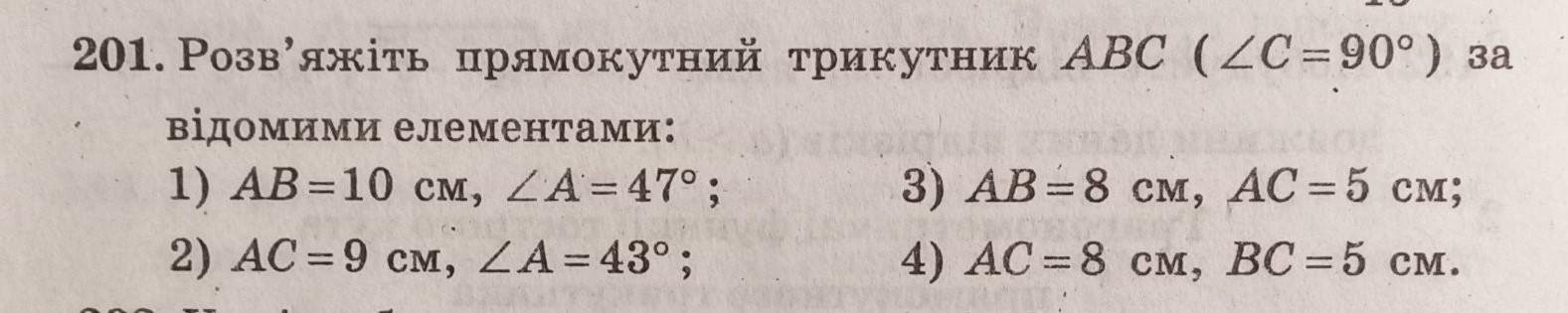
Ответы
Відповідь:
Пояснення:
1)
AB=10 см, <A=47°.
За теоремою синусів в прямокутному трикутнику:
AB/sin A = AC/sin C,
де AC - гіпотенуза, C - прямий кут.
Знаходимо значення гіпотенузи:
AC = AB/sin A * sin C = 10 см / sin 47° * sin 90° = 12,67 см.
Тепер застосовуємо теорему Піфагора для знаходження другого катета:
BC^2 = AC^2 - AB^2
BC = √(AC^2 - AB^2) = √((12,67 см)^2 - (10 см)^2) ≈ 6,35 см.
Отже, другий катет дорівнює близько 6,35 см.
Таким чином, прямокутний трикутник ABC з катетами AB=10 см і BC≈6,35 см має гіпотенузу AC≈12,67 см.
2)
AC = 9 см, <A=43°.
За теоремою синусів в прямокутному трикутнику:
AC/sin C = AB/sin B,
де AB - катет прямокутного трикутника, B - кут при вершині B.
Оскільки С=90°, то sin C = 1. Тоді маємо:
AB = AC * sin B / sin C = 9 см * sin 43° / sin 90° ≈ 6,15 см.
Тепер застосуємо теорему Піфагора, щоб знайти другий катет:
BC^2 = AC^2 - AB^2
BC = √(AC^2 - AB^2) = √((9 см)^2 - (6,15 см)^2) ≈ 4,39 см.
Отже, прямокутний трикутник ABC з катетами AB≈6,15 см і BC≈4,39 см має гіпотенузу AC=9 см.