Яке з наведених тверджень неправильне
1 діагоналі прямокутника рівні
2 діагоналі паралелограма є бісектрисами його кутів
3діагоналі ромба взаємно перпендикулярні
4 діагоналі квадрата перетинаються під прямим кутом
Срооооочно!!!!!!!!! Даю 100 балів
Ответы
Ответ:
Утверждение номер 2 - неверное.
Объяснение:
- Разберем каждое утверждение.
1. "Диагонали прямоугольника равны". Данное утверждение верное, поскольку диагонали любого произвольного прямоугольника равны. Доказательство:
Пусть нам дан прямоугольник ABCD (рис. 1). Проведем две диагонали AC и BD. Рассмотрим треугольники ABD и ABC:
1) ∠DAB = ∠ABC = 90° (по опр. прямоугольника);
2) AB - общий катет обоих треугольников;
3) AD = BC (по опр. прямоугольника).
Этих условий достаточно, чтобы заявить, что Δ ABD = Δ ABC. Тогда их гипотенузы так же будут равны, то есть AC = BD!
2. "Диагонали параллелограмма являются биссектрисами его углов". Данное утверждение неверное, поскольку оно выполняется лишь для частного случая параллелограмма, а именно для ромба(квадрата).
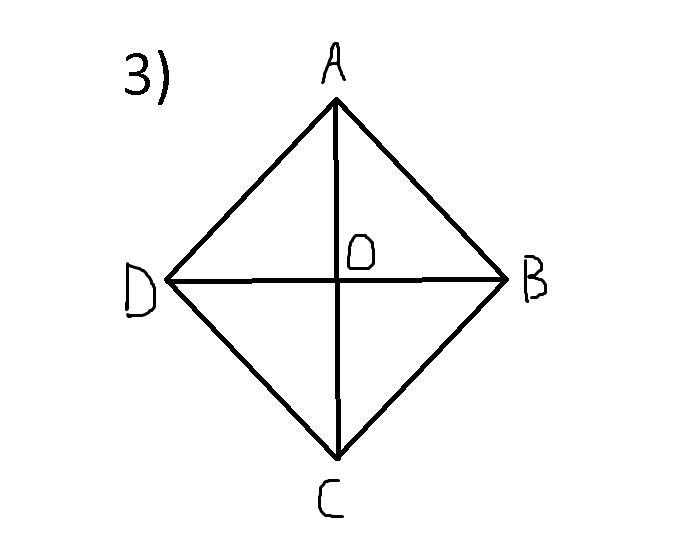
3. "Диагонали ромба взаимно перпендикулярны". Данное утверждение верное, поскольку пересечения диагоналей любых ромбов образуют угол в 90°. Доказательство:
Пусть нам дан ромб ABCD (рис. 3). Проведем диагонали AC и DB. По определению параллелограмма, точка пересечения диагоналей AC и DB делит их пополам. Обозначим ее за O.
1) AD = AB (по опр. ромба), значит ABD - равнобедренный;
2) AO - медиана, проведенная к DB (основанию). По св-вам равнобедренного треугольника, данная медиана будет одновременно являться и высотой.
3) Из предыдущего условия получаем, что ∠AOB = ∠AOD = 90°, а это означает, что AC и BD - взаимно перпендикулярные отрезки!
4. "Диагонали квадрата пересекаются под прямым углом". Данное утверждение верное. Поскольку квадрат - частный случай ромба, это значит, что к нему применимо то же доказательство о взаимной перпендикулярности диагоналей, что и для ромба (возвращаемся к доказательству номер 3).