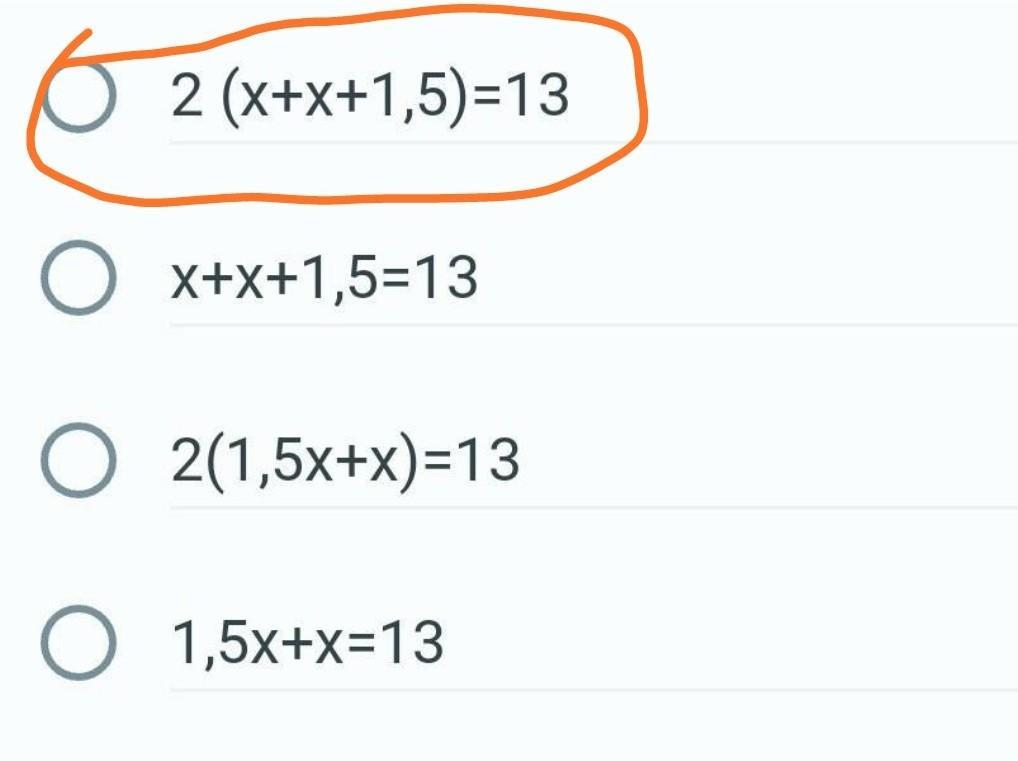Яке рівняння відповідає умові задачі ? Периметр прямокутника дорівнює 13см, а одна з його сторін на 1,5 см більша за сусідню. знайти сторони прямокутника.
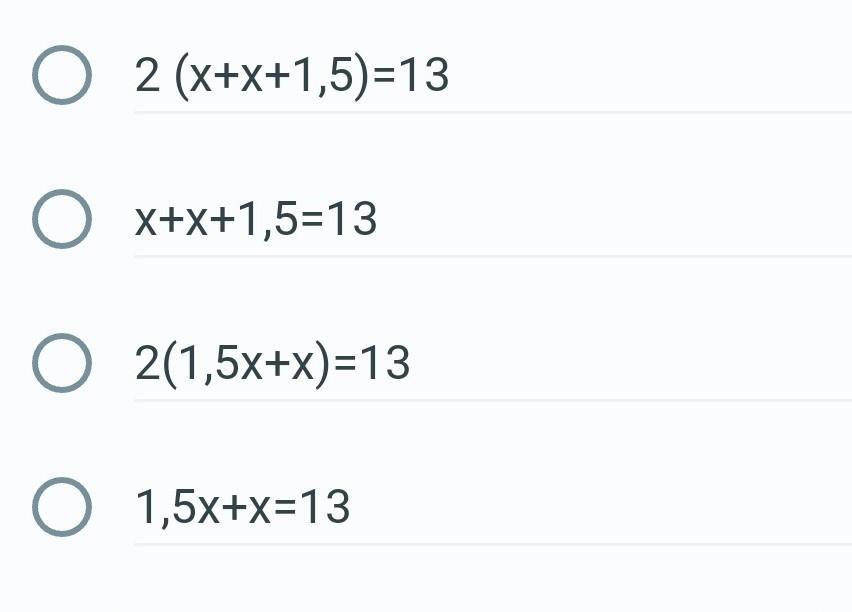
Ответы
Ответ:Припустимо, що одна сторона прямокутника дорівнює x см, тоді інша сторона буде (x + 1,5) см.
За умовою задачі, периметр прямокутника дорівнює 13 см, тому можемо записати рівняння на основі формули для периметру прямокутника:
2 * (довжина + ширина) = 13
Підставляємо вирази для довжини та ширини прямокутника:
2 * (x + (x + 1,5)) = 13
Спрощуємо вираз, розкриваємо дужки:
2 * (2x + 1,5) = 13
Поділимо обидві частини рівняння на 2:
4x + 3 = 13
Віднімемо 3 від обох частин рівняння:
4x = 13 - 3
4x = 10
Розділимо обидві частини рівняння на 4, щоб виразити x:
x = 10 / 4
x = 2,5
Отже, одна сторона прямокутника дорівнює 2,5 см, а друга сторона (ширина) буде 2,5 + 1,5 = 4 см.
Пошаговое объяснение:Значит получаетса второе
Ответ:
Пошаговое объяснение:
1 сторона = х
2 сторона = х + 1,5
Р = 13
2(х + х + 1,5) = 13
2(2х + 1,5) = 13
4х + 3 = 13
4х = 13 - 3
4х = 10
х = 10 : 4
х = 2,5
1 сторона = (х) = 2,5 см
2 сторона = (х + 1,5) = 2,5 + 1,5 = 4 см