Предмет: Математика,
автор: lazarevdatacentre
Знайдіть границі функції за допомоги Другої чудової
Приложения:
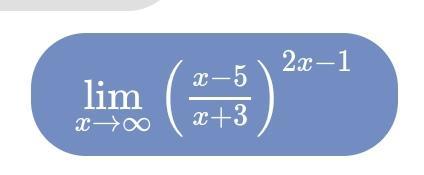
Ответы
Автор ответа:
1
Ответ .
Второй замечательный предел : .
Приложения:

Похожие вопросы
Предмет: Английский язык,
автор: 1512
Предмет: Русский язык,
автор: javohirrahimov1991
Предмет: Геометрия,
автор: robertpolson330
Предмет: Химия,
автор: player680igrok
Предмет: Химия,
автор: diiaasha