Предмет: Геометрия,
автор: vvdkfy
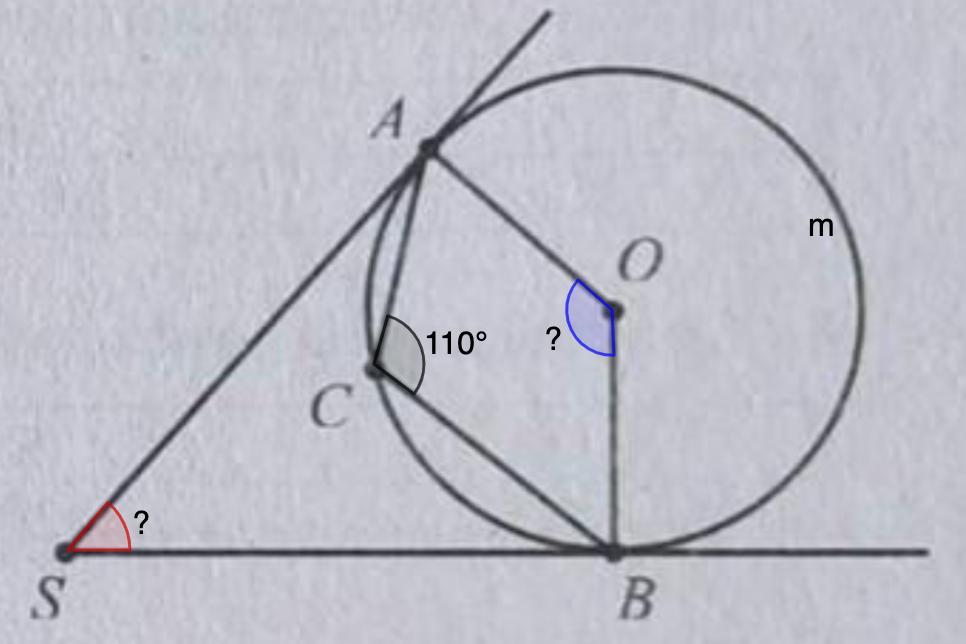
На схематичному рисунку зображено точку S, коло з центром у точці О і дві дотичні SA та SB, проведені з точки S до кола. Точки А, В,С належать колу. Відомо, що ZACB=110°. Знайдіть градусні міри кутів: 1) AOB; 2) ASB.
Приложения:

Ответы
Автор ответа:
2
Ответ:
1) ∠AOB = 140°; 2) ∠ASB = 40°.
Объяснение:
9. На схематическом рисунке показана точка S, окружность с центром в точке О и две касательные SA и SB, проведенные из точки S к окружности. Точки А, В, С принадлежат окружности. Известно, что ∠ACB=110°. Найдите градусные меры углов: 1) ∠AOB; 2) ∠ASB.
Дано: Окр.О;
SA и SB - касательные;
А, В, С ⊂ Окр.О;
∠ACB = 110°.
Найти: 1) ∠AOB; 2) ∠ASB.
Решение:
1) ∠АСВ = 110° - вписанный.
- Вписанный угол измеряется половиной градусной меры дуги, на которую он опирается.
⇒ ◡AmB = 2 · 110° = 220°
- Градусная мера окружности равна 360°.
⇒ ◡АСB = 360° - ◡AmB = 360° - 220° = 140°
- Центральный угол равен градусной мере дуге, на которую он опирается.
⇒ ∠AOB = ◡АСB = 140°
2) SA и SB - касательные.
- Угол между двумя касательными, проведенными из одной точки, равен полуразности большей и меньшей высекаемых ими дуг.
∠ASB = (◡AmB - ◡ACB) : 2 = (220° - 140°) : 2 = 40°
#SPJ1
Приложения:
Похожие вопросы
Предмет: История,
автор: kairlanlt
Предмет: Алгебра,
автор: milanageld25
Предмет: Химия,
автор: irzyrianova313
Предмет: Українська література,
автор: Marysin
Предмет: Английский язык,
автор: fyyfuufu