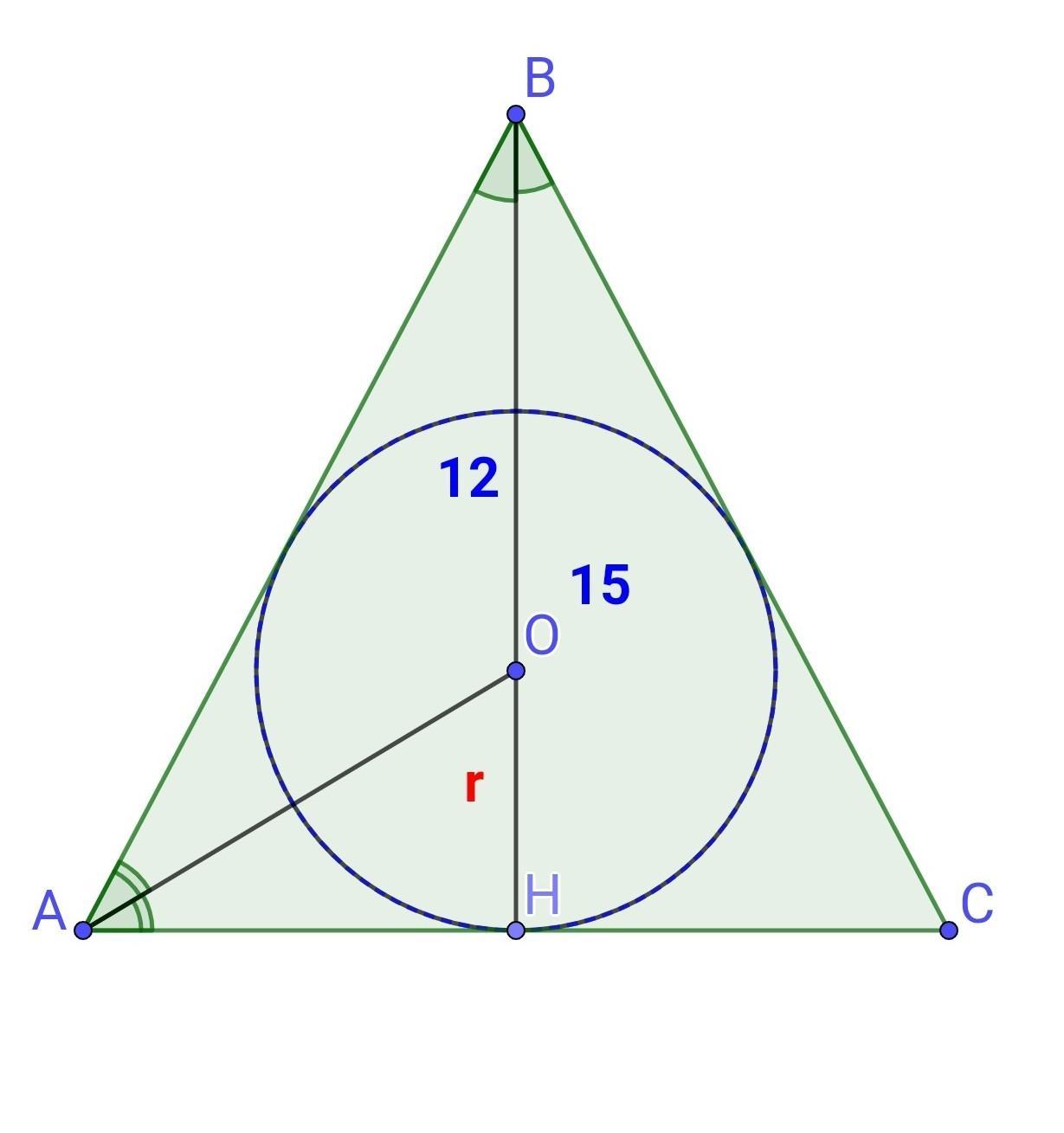
У рівнобедреному трикутнику висота, проведена до основи, дорівнює 15 см, а центр вписаного кола віддалений від вершини, яка протилежна основі, на 12 см. Знайдіть діаметр вписаного кола.
Ответы
Ответ:
Діаметр вписаного кола дорівнює 6 см
Объяснение:
У рівнобедреному трикутнику висота, проведена до основи, дорівнює 15 см, а центр вписаного кола віддалений від вершини, яка протилежна основі, на 12 см. Знайдіть діаметр вписаного кола.
В рівнобедреному трикутнику ABC маємо: АВ = BC, BH - висота, BH⟂AC, ВН=15 см. О - центр вписаного кола. Знайдемо діаметр вписаного кола.
РОЗВ'ЯЗАННЯ
- Центр вписаного кола лежить в точці перетину бісектрис трикутника.
В рівнобедреному трикутнику висота буде також бісектрисою кута трикутника, з вершини якого вона проведена. Тому центр вписаного кола О лежить на висоті ВН.
За умовою центр вписаного кола віддалений від вершини, яка протилежна основі, на 12 см. Отже ВО=12 см.
ОН - радіус вписаного кола.
r=ОН=ВН-ВО=15-12=3(см)
Діаметр кола удвічі довший за радіус, тому:
d=2•r=2•3=6(см)
Відповідь: 6 см
#SPJ1