Предмет: Математика,
автор: vzam
Знайти частинний розв’язок диференціального рівняння. (y=uv, y’=u’v+uv’)
Приложения:
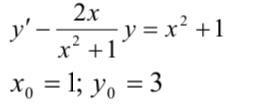
Ответы
Автор ответа:
1
Ответ:
Частное решение дифференциального уравнения:
Пошаговое объяснение:
- линейное дифференциальное уравнение первого порядка
1)
---------------------------------------------------------------------------------------------------------
- не является решением дифференциального уравнения
---------------------------------------------------------------------------------------------------------
Пусть
Решением дифференциального уравнения есть функция:
Частное решение при условии
- частное решение дифференциального уравнения при заданных начальных условиях
Похожие вопросы
Предмет: Другие предметы,
автор: bpikaluk79
Предмет: ОБЖ,
автор: kuharveronica
Предмет: Литература,
автор: kaliyznaanna12
Предмет: Русский язык,
автор: rmsh0919890
Предмет: Математика,
автор: dqdqwdqwdqdq123