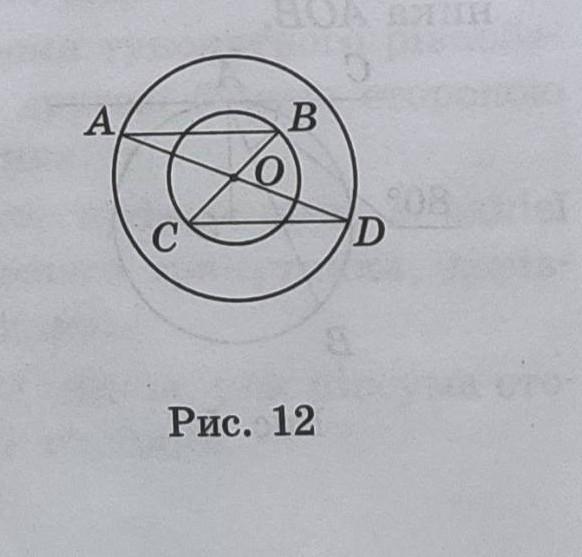
За рисунком. 12 доведіть, що AB||CD (О-центр кіл)
(За рисунком 12 доведите что АВ||СD, О-центр кола)
Поможіть будь ласка!!
Ответы
Ответ:
Объяснение: Угол ВАД измеряется половиной разности двух дуг которые он отсекает на меньшей окружности. Учитывая равенство центральных углов в меньшей окружности угол ВОД=АОС, а значит и соответственно дуг, на которые они опираются, аналогично, равны углы и дуги, на которые они опираются угол АОВ =СОД. Расмотрим треугольники АОВ и СОД : АО=ОД как радиусы большей окружности, ОВ=ОС как радиусы меньшей окружности, угол СОД=АОВ (мы выше это установили), значит, треугольники АОВ и СОД равны по двум сторонам и углу между ними. Против равных сторон в треугольниках лежат равные углы. Учитывая, что ОС=ОВ как радиусы меньшй окружности, делаем вывод что угол ОДС = ВАО. Теперь на наш рисунок посмотрим с другой стороны: Две прямые АВ и СД пересекаются секущей их прямой АД, при этом углы АДС, он же ОДС, и угол ВАД , он же ВАО, равны и являются в этом рисунке внутренними накрест лежащими углами. По теореме, обратной к теореме о двух параллельных прямых, которые пересекаются третьей, делаем вывод, что прямые АВ и СД параллельны, что и трбовалось доказать.