Дана правильная четырёхугольная пирамида PABCD с вершиной P и основанием ABCD. Длина стороны основания пирамиды PABCD равна 1, а длина бокового ребра равна 2. Сфера с центром в точке O касается плоскости (ABC) в точке A и касается бокового ребра PB. Найдите объём пирамиды OABCD. Ответ округлите до сотых.
!Очень желательно с чертежом и полным объяснением!
Ответы
Все прямые в плоскости ABC через точку касания A являются касательными к сфере.
BA - касательная к сфере
К - точка касания на ребре PA
BK и BA - отрезки касательных из одной точки, BK=BA=1
На сфере есть окружность, касающаяся сторон угла PBA в точках K и A.
T - центр этой окружности
Центр сферы O лежит
- на перпендикуляре к (PBA) через центр T
- на перпендикуляре к (ABC) через точку A
OA - радиус сферы и высота искомой пирамиды.
Центр T лежит на биссектрисе угла PBA
cosB =AB/2 : PB =1/4
tg(B/2) =√(1-cosa / 1+cos) =√(3/5)
TA =AB tg(B/2) =√(3/5)
Понятно, что грань PBA одинаково наклонена к перпендикуляру OA и высоте пирамиды PH.
Тогда угол AOT равен углу наклона грани к основанию.
PM - апофема, ∠AOT=∠PMH
CH=√2/2 ; PH=√(16-2)/2 =√14/2
MH=1/2 ; PM=√(14+1)/2 =√15/2
sin(AOT) =sin(PMH) =PH/PM =√(14/15)
OA =TA/sin(AOT) =√(3/5) : √(14/15) =3/√14
V(OABCD) =1/3 So OA =1/3 *1 *3/√14 =1/√14
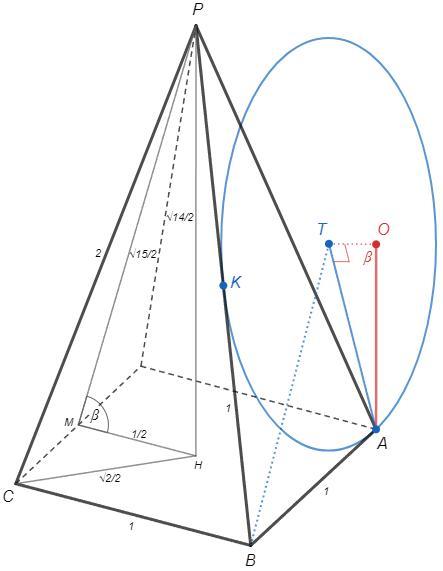
К - точка касания на ребре PA"