Предмет: Алгебра,
автор: masha01021
Помогите пожалуйста ,вычислить интеграл
Приложения:
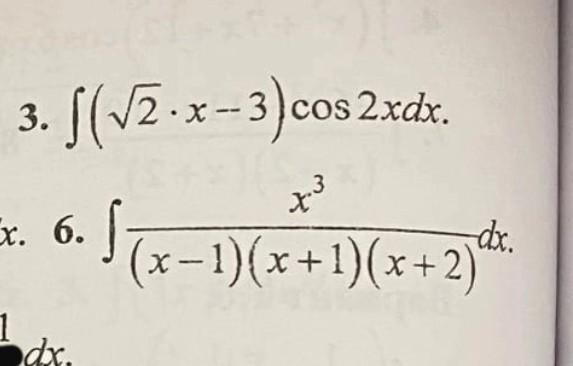
Ответы
Автор ответа:
1
Объяснение:
попробуйте предложенный вариант; ответы подчёркнуты цветным.
Приложения:

mazelov:
помогите пожалуйста с алгеброй у меня в профиле
буду очень благодарен
Автор ответа:
1
Ответ:
Объяснение:
Вычислить интеграл:
1.
Интегрирование по частям:
2.
Преобразуем подинтегральное выражениие.
Выделим целую часть:
Получим сумму интегралов:
Вычислим второй интеграл, представив подинтегральное выражение в виде суммы простейших дробей:
Избавимся от знаменателя:
Сравним коэффициенты при одинаковых степенях х, решим систему уравнений:
из второго уравнения:
подставим в первое:
В и С подставим в третье:
а выше не правильно?
проверьте ответы пожалуйста
вверху правильно, одобрено экспертом
Похожие вопросы
Предмет: Українська мова,
автор: sofiyaperepelytsiya2
Предмет: Українська мова,
автор: nelianikita1994
Предмет: Русский язык,
автор: katia67892
Предмет: Литература,
автор: vkurockina668
Предмет: ОБЖ,
автор: gnohbi