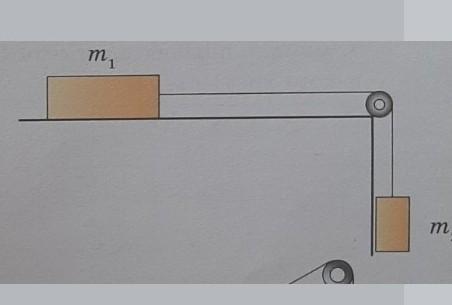
На куті стола закріпили блок, через який перекинули нитку. До кінців нитки прикріпи- ли два вантажі. Маса першого вантажу до- рівнює 600 г. Якої максимальноï маси може бути другий вантаж, щоб обидва вантажі за- лишалися в стані спокою? Коефіцієнт тертя першого вантажу об поверхню дорівнює 0,4.
Ответы
Ответ:
m2 ≤ -0.24 кг
Объяснение:
Для того, щоб обидва вантажі залишалися в стані спокою, необхідно, щоб сила натягу нитки була достатньою, щоб перебороти силу тертя між першим вантажем та столом.
Сила тертя між першим вантажем та столом дорівнює:
Fтертя = μ * N
де μ - коефіцієнт тертя, N - сила тиску вантажу на стіл.
Так як вантаж першого вантажу стаціонарний, сила тиску дорівнює силі тяжіння:
N = m1 * g
де m1 - маса першого вантажу, g - прискорення вільного падіння.
Тоді сила тертя може бути записана як:
Fтертя = μ * m1 * g
З іншого боку, сила натягу нитки має бути достатньою, щоб утримувати обидва вантажі в стані спокою. Так як обидва вантажі залишаються в стані спокою, сила натягу в нитці має бути однаковою на обох кінцях. Тому, якщо другий вантаж має масу m2, сила натягу дорівнює:
Fнатягу = m1 * g + m2 * g
Для того, щоб знайти максимальну масу другого вантажу, потрібно, щоб сила натягу була достатньою, щоб перебороти силу тертя. Тобто:
Fнатягу ≥ Fтертя
m1 * g + m2 * g ≥ μ * m1 * g
m2 ≤ (μ - 1) * m1
Підставляючи відомі значення, ми отримуємо:
m2 ≤ (0.4 - 1) * 0.6 кг
m2 ≤ -0.24 кг
Отже, максимальна маса другого вантажу, при якій обидва вантажі залишаються в стані спокою, не може бути від'ємною. Отже, максимальна маса другого вантажу - 0 кг. Другий вантаж повинен бути невагомим.