Предмет: Геометрия,
автор: maksimcukbogdan3
1. У прямокутному трикутнику один з катетів дорівнює 15 см, а проекція іншого катета
на гіпотенузу 16 см. Знайдіть периметр трикутника.
Ответы
Автор ответа:
0
Ответ:
Периметр трикутника дорівнює 60 см
Объяснение:
У прямокутному трикутнику один з катетів дорівнює 15 см, а проекція іншого катетана гіпотенузу 16 см. Знайдіть периметр трикутника
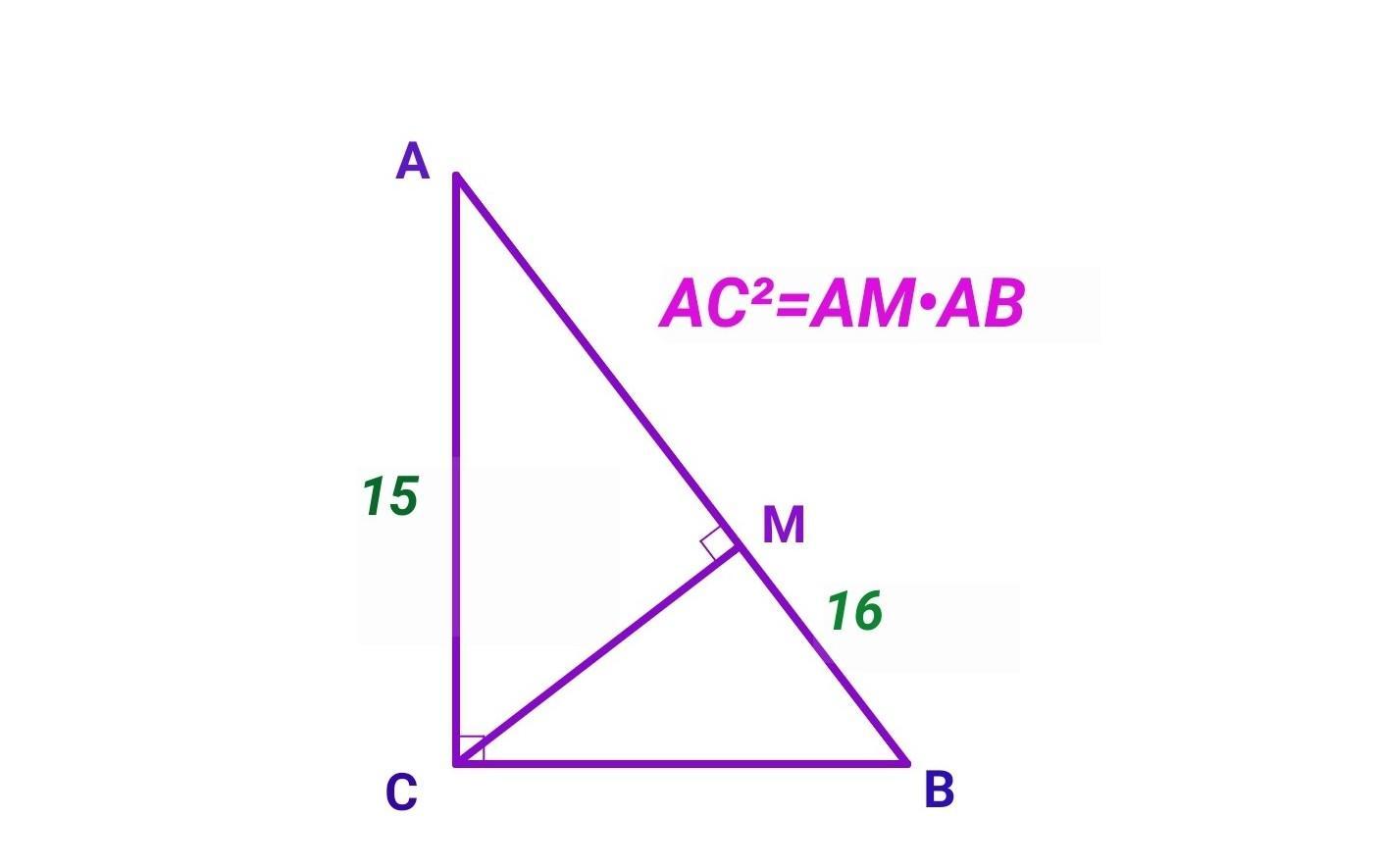
Нехай АВС - даний прямокутний трикутник (∠С=90°). Катет АС =15 см. СМ⟂АВ. МВ - проекція катета ВС на гіпотенузу АВ. MB=16 см.
1) За метричними співвідношеннями у прямокутному трикутнику маємо:
AC²=AB•AM
Позначимо AM=х (см), тоді AB=AM+MB=x+16 (см). Маємо:
15²=(х+16)х
х²+16х-225=0
За теоремою Вієта отримаємо два корені: х₁=-25 (не задовольняє умові задачі), х₂=9
Отже AM=9(см), а AB=9+16=25(см)
2) За теоремою Піфагора знайдемо катет BC:
BC²=AB²-AC²
BC²=25²-15²=625-225=400
BC=20(см)
3) Периметр трикутника дорівнює сумі всіх його сторін:
Р(ABC)=AB+BC+AC=25+20+15=60(см)
Відповідь: 60 см
Приложения:
ГАЗ52:
Описка "х₁=-12(не задовольняє умові задачі)"
Спасибо. Исправила
Похожие вопросы
Предмет: Русский язык,
автор: aaulymbubkir
Предмет: Биология,
автор: netikanevz
Предмет: Математика,
автор: sumayyanabiyeva8
Предмет: Математика,
автор: NoName2994