Розв'яжіть рівняння 3(x^2+1/x^2)+2(x+1/x)=10
За теоремою Вієта зі змінною t або за дискримінантом
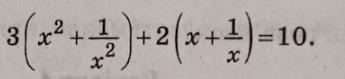
Ответы
Ответ:
Почнемо з введення нової змінної. Припустимо, що t = x + 1/x. Тоді ми можемо виразити деякі вирази з початкового рівняння в термінах змінної t.
Замінимо вирази x + 1/x на t в початковому рівнянні:
3(x^2 + 1/x^2) + 2(x + 1/x) = 10
3t^2 + 2t = 10
Спочатку приведемо рівняння до стандартного вигляду:
3t^2 + 2t - 10 = 0
Застосуємо квадратну формулу:
t = (-b ± √(b^2 - 4ac)) / (2a),
де a = 3, b = 2 і c = -10.
Підставляємо
t = (-2 ± √(2^2 - 4 * 3 * -10)) / (2 * 3)
t = (-2 ± √(4 + 120)) / 6
t = (-2 ± √124) / 6
t = (-2 ± 2√31) / 6
t = (-1 ± √31) / 3
Таким чином, ми отримали два рішення для змінної t: (-1 + √31) / 3 і (-1 - √31) / 3.
Оскільки ми вводили замінну t = x + 1/x, тепер ми можемо підставити назад вирази для x + 1/x:
x + 1/x = (-1 + √31) / 3
або
x + 1/x = (-1 - √31) / 3