Предмет: Геометрия,
автор: dizzlike2000
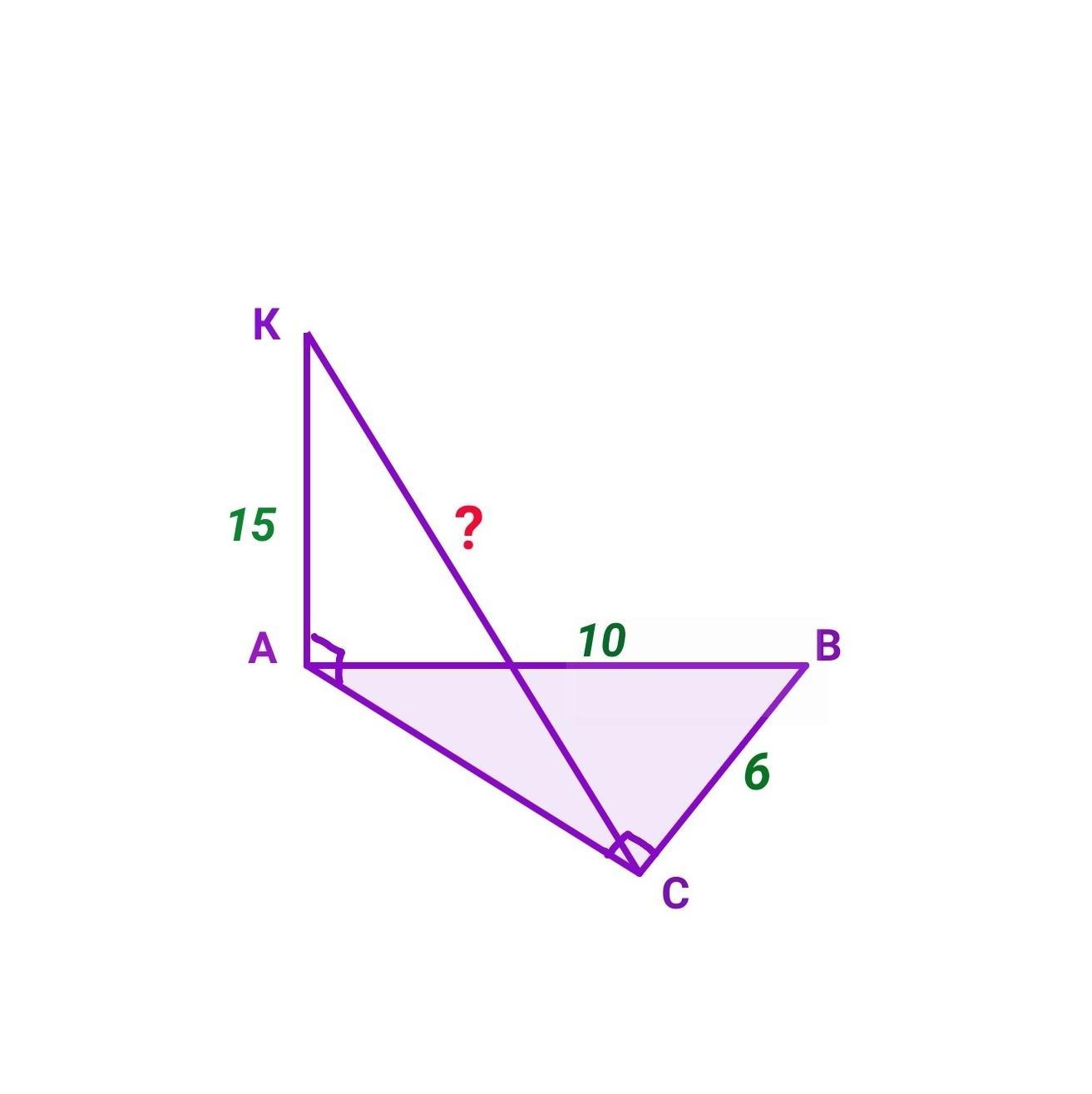
AK - перпендикуляр до площини прямокутного трикутника ABC, кут С = 90 градусов. Обчислити КС, якщо АВ=10 см, СВ=6 см, АК=15 см.
Ответы
Автор ответа:
2
Ответ:
КС=17 см
Объяснение:
AK - перпендикуляр до площини прямокутного трикутника ABC, кут С = 90 градусов. Обчислити КС, якщо АВ=10 см, СВ=6 см, АК=15 см.
За умовою AK⟂(ABC), тому (за властивістю) вона перпендикулярна до кожної прямої, що належить площині АВС, тобто AK⟂AC, отже △KAC - прямокутний.
1) Розглянемо прямокутний трикутник АВС (∠С=90°).
AB=10 см - гіпотенуза, ВС=6 см - катет.
За теоремою Піфагора знайдемо катет АС
AC²=AB²-BC²
AC²=10²-6²=100-36=64
AC=8(см)
2) Розглянемо прямокутний трикутник КАС(∠А=90°)
Катет АК=15 см, катет АС=8 см.
За теоремою Піфагора знайдемо гіпотенузу КС:
КС²=АК²+АС²
КС²=15²+8²=225+64=289
КС=17(см)
Відповідь: 17 см
#SPJ1
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: sasha7256sasha
Предмет: История,
автор: Yaroslav1620
Предмет: Қазақ тiлi,
автор: myrzamatdaryn6
Предмет: Математика,
автор: Аноним
Предмет: Английский язык,
автор: Minitroll