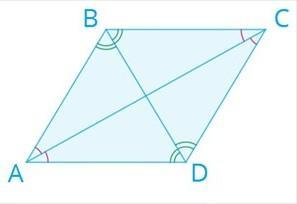
Диагонали ромба равны 12 см и 16 см.
Вычислите длину стороны ромба!
Ответы

d1 = BD = 12 см – первая диагональ
d2 = AC = 16 см – вторая диагональ
Пусть точка посередине ромба это точка О
Свойство диагоналей в ромбе гласит: Диагонали в ромбе пересекаются и точкой пересечения делятся пополам, а также что диагонали ромба перпендикулярны друг другу. Это значит, что проведя Диагонали в ромбе, мы образуем четыре прямоугольных треугольника. Рассмотрим треугольник АОВ
АО = 1/2АС = 16/2 = 8 см(по свойству диагоналей в ромбе)
ВО = 1/2ВD = 12/2 = 6 см(по тому же свойству диагоналей в ромбе)
Вспомним теорему Пифагора, которая гласит, что квадрат гипотенузы равен сумме квадратов катетов. Это значит, что АВ²(гипотенуза в квадрате) = АО² + ВО²
АВ² = 8² + 6²
АВ² = 64 + 36
АВ² = 100
АВ² = 10²
Сокращаем квадраты
АВ = 10 (см)
По определению ромба, все стороны ромба равны
Ответ: 10 см – длина стороны ромба
Рад помочь!