Предмет: Математика,
автор: rkia978
Гениальные математики, помогите, пожалуйста!
Нужно решение.
Это очень срочно...
[Не пишите чепуху!]
Приложения:
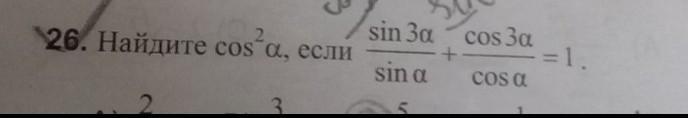
Ответы
Автор ответа:
3
Ответ:
cos²α = 5/8
Пошаговое объяснение:
Левую часть напишем над общим знаменателем :
В числителе получаем синус суммы sin(x+y) = sinx·cosy+cosx·siny :
По формуле двойного угла cos2α = 2cos²α-1 , тогда:
Мозгокошка:
Здравствуйте!Простите за то,что возможно слишком часто прошу помочь мне..,но снова нужна помощь с заданиями по алгебре.Я была бы очень благодарна Вам за помощь.Прошу Вас ,если вы не заняты,есть время,силы то помогите мне пожалуйста.Задание в моем профиле.В любом случае спасибо и хорошего Вам дня
Похожие вопросы
Предмет: История,
автор: anastasia136919
Предмет: Геометрия,
автор: noreplys300
Предмет: Другие предметы,
автор: sultannochka0
Предмет: Математика,
автор: mixailov99