Предмет: Алгебра,
автор: Danyl228
Помогите срочно
Знайти треба екстремуми функції f(x) = (x^2+5) /(2-x)
Ответы
Автор ответа:
2
Ответ:
Приложения:
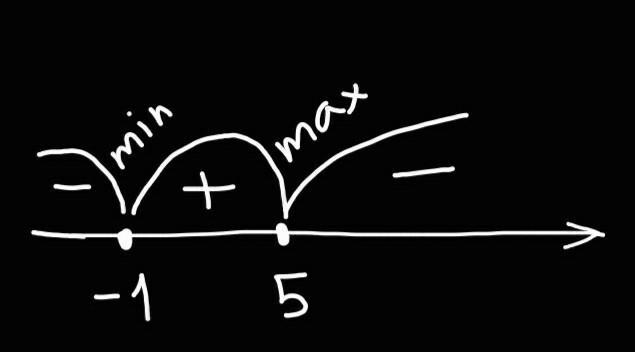
Похожие вопросы
Предмет: Физика,
автор: tanzura7
Предмет: Українська мова,
автор: E3gor
Предмет: Биология,
автор: artemkuprienko1708
Предмет: Қазақ тiлi,
автор: sydyknazarr0963
Предмет: Алгебра,
автор: Ruslana8767