(cos 2a)/(cos a - sin a)
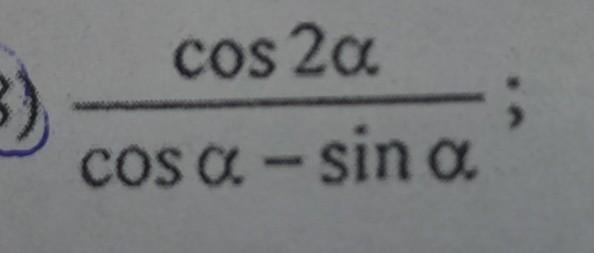
Ответы
Ответ:
Используем формулу двойного угла для косинуса:
cos 2a = 2 cos² a - 1
Теперь заменим cos 2a в числителе:
(cos 2a) / (cos a - sin a) = (2 cos² a - 1) / (cos a - sin a)
Разложим числитель на две дроби и сократим общий множитель:
(2 cos² a - 1) / (cos a - sin a) = [(2 cos a + 1) + (2 cos a - 1)] / (cos a - sin a)
= (2 cos a + 1)/(cos a - sin a) + (2 cos a - 1)/(cos a - sin a)
Таким образом, выражение можно упростить до двух дробей:
(cos 2a) / (cos a - sin a) = (2 cos a + 1)/(cos a - sin a) + (2 cos a - 1)/(cos a - sin a)
Можно заметить, что обе дроби имеют одинаковый знаменатель, поэтому их можно сложить:
(cos 2a) / (cos a - sin a) = [(2 cos a + 1) + (2 cos a - 1)] / (cos a - sin a)
= (4 cos a) / (cos a - sin a)
Ответ: (cos 2a) / (cos a - sin a) = (4 cos a) / (cos a - sin a)