..............................

Ответы
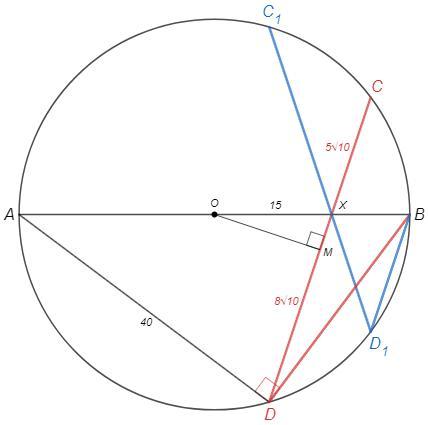
∠ADB=90. Отрезок AB виден из точки D под прямым углом, следовательно точка D лежит на окружности диаметром AB.
∠DCB=∠DAB. Отрезок DB виден из точек C и A под равным углом, следовательно точки D-A-C-B лежат на одной окружности.
Т.е. xорда СD пересекает диаметр AB в точке X.
CD/AB =13√10/50
Пусть CD=13√10 ; AB=50
AX/BX=4
Тогда AX=40 ; BX=10
AX*XB=CX*XD (т об отрезках пересекающихся хорд)
CX и XD - корни
т Виета: CX+XD=13√10 ; CX*XD=40*10
t^2 -13√10 t +400 =0 => t= 13√10+-3√10 /2
={5√10; 8√10}
Имеем два решения - CD и D1С1 - симметричных относительно AB.
Нас интересуют углы CDB и C1D1B.
◡C1B=◡DB => ∠C1D1B=∠DAB
OM⊥CD (перпендикуляр из центра к хорде), CM=CD/2
MX =CM-CX =13√10/2 -5√10 =3√10/2
OX=OB-BX=25-10=15
cos(OXM) =MX/OX =3√10/2*15 =1/√10
△DAX, т косинусов
AD^2 =AX^2+DX^2-2AX*DX*cosX =1600+640-2*40*8√10/√10 =1600
=> AD=40
cos(DAB)=AD/AB=4/5 => △ABD - египетский => tg(DAB)=3/4 =tg(C1D1B)
AD=AX, △DAX-р/б
A/2 =90-∠ADX =∠CDB
tg(CDB) =tg(A/2) =(1-cosA)/sinA =(1 -4/5) :3/5 =1/3
Ответ: tg(CDB)+tg(C1D1B) =1/3 +3/4 =13/12