Question

100 БАЛЛОВ ПОМОГИТЕ СРОЧНО С АЛГЕБРОЙ

ВЫЧИСЛИТЕ sin2a,если:​

Answer 1

$\displaystyle\bf\\1)\\\\Sin\alpha =\frac{3}{5} \\\\\frac{\pi }{2} < \alpha < \pi \ \ \ \Rightarrow \ \ \ Cos\alpha < 0\\\\\\Cos\alpha =-\sqrt{1-Sin^{2}\alpha } =-\sqrt{1-\Big(\frac{3}{5} \Big)^{2} }=\\\\\\=-\sqrt{1-\frac{9}{25} } =-\sqrt{\frac{16}{25} } =-\frac{4}{5} \\\\\\Sin2\alpha =2\cdot Sin\alpha \cdot Cos\alpha =2\cdot \frac{3}{5} \cdot \Big(-\frac{4}{5} \Big)=-\frac{24}{25} =-0,96\\\\\\Otvet \ : \ Sin2\alpha =-0,96$

$\displaystyle\bf\\2)\\\\Cos\alpha =-\frac{4}{5} \\\\\pi < \alpha < \frac{3\pi }{2} \ \ \ \Rightarrow \ \ \ Sin\alpha < 0\\\\\\Sin\alpha =-\sqrt{1-Cos^{2}\alpha } =-\sqrt{1-\Big(-\frac{4}{5} \Big)^{2} }=\\\\\\=-\sqrt{1-\frac{16}{25} } =-\sqrt{\frac{9}{25} } =-\frac{3}{5} \\\\\\Sin2\alpha =2\cdot Sin\alpha \cdot Cos\alpha =2\cdot \Big(-\frac{3}{5} \Big)\cdot \Big(-\frac{4}{5} \Big)=\frac{24}{25} =0,96\\\\\\Otvet \ : \ Sin2\alpha =0,96$

Answer 2

Ответ:

a) sin2α = - 24/25

б) sin2α = 24/25

Объяснение:

a)

Дано:

sinα = 3/5 , π/2 < α < π

Найти:

sin2α

Решение:

$\boxed{ \sin2 \alpha =2 \sin \alpha \cos \alpha }$

Воспользуемся основным тригонометрическим тождеством sin²α + cos²α = 1 и найдем cosα:

$\displaystyle \left ( \frac{3}{5} \right) {}^{2} + \cos {}^{2} \alpha = 1 \\ \\ \cos \alpha = \pm \sqrt{1 -\left ( \frac{3}{5} \right) {}^{2} } = \pm \sqrt{1 - \frac{9}{25} } = \\ \\ = \pm \sqrt{ \frac{16}{25} } = \pm \frac{4}{5}$

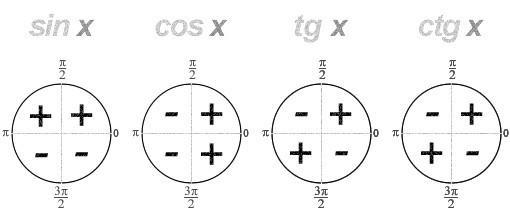
По условию угол альфа принадлежит второй четверти , где собственно косинус угла должен быть отрицательным. Следовательно :

$\displaystyle \cos \alpha = - \frac{4}{5}$

Находим синус двойного угла:

$\displaystyle \sin2 \alpha = 2 \cdot \frac{3}{5} \cdot \left ( - \frac{4}{5} \right) = - \frac{24}{25}$

б)

Дано:

cosα = -4/5 , π < α < 3π/2

Найти:

sin2α

Решение:

$\displaystyle \sin {}^{2} \alpha + \left ( - \frac{4}{5} \right) {}^{2} = 1 \\ \\ \sin \alpha = \pm \sqrt{1 -\left ( - \frac{4}{5} \right) {}^{2} } = \pm \sqrt{1 - \frac{16}{25} } \\ \\ = \pm \sqrt{ \frac{9}{25} } = \pm \frac{3}{5}$

Тут по условию угол альфа принадлежит третьей четверти, где синус угла должен принимать отрицательные значения. Следовательно :

$\displaystyle \sin \alpha = - \frac{3}{5}$

По синусу двойного угла :

$\displaystyle \sin2 \alpha = 2 \cdot\left ( - \frac{4}{5} \right) \cdot\left ( - \frac{3}{5} \right) = \frac{24}{25}$