Question

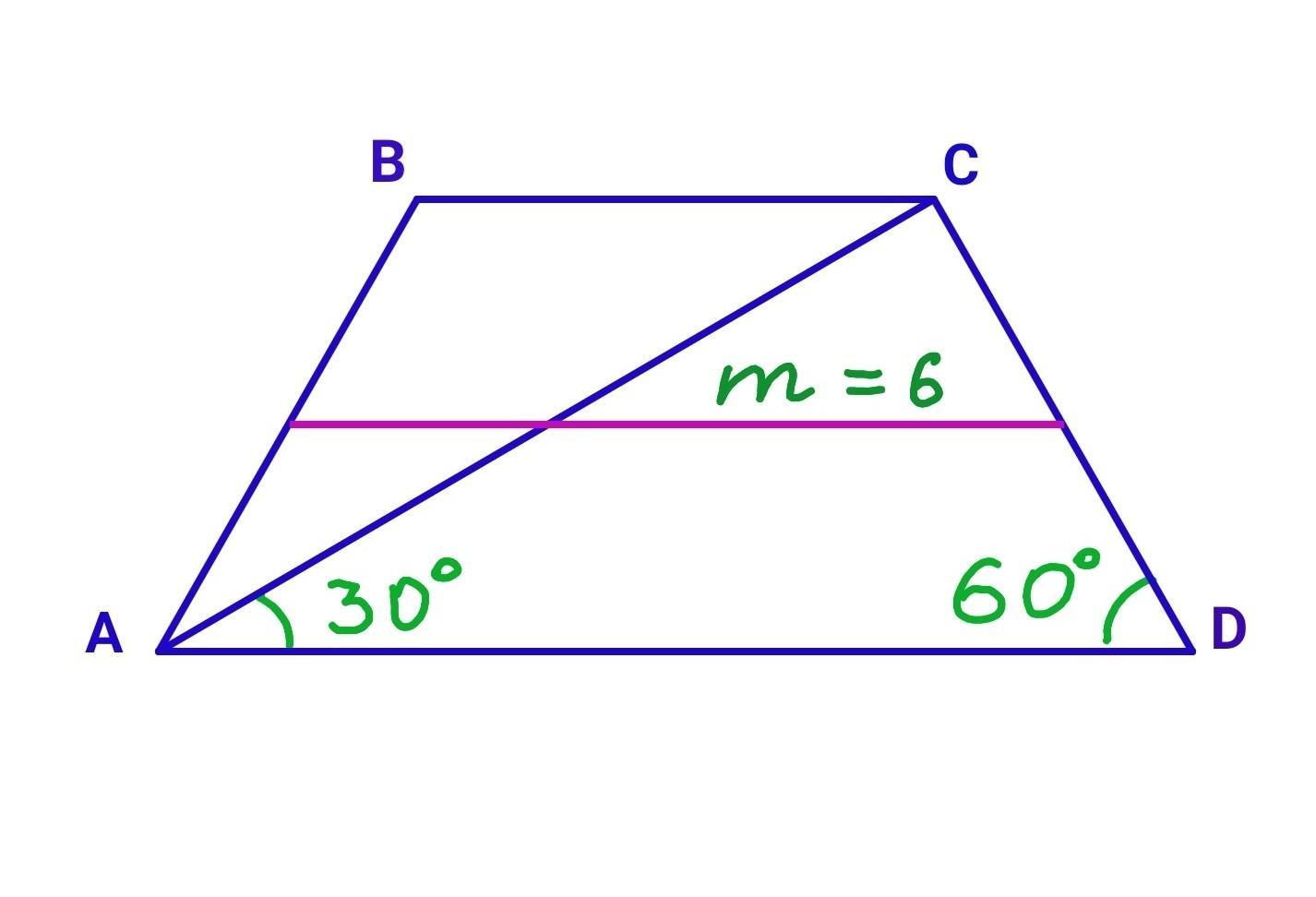
9.Средняя линия равнобедренный трапеции равна 6 см. Диагональ образуется с большим основанием угол 30°. Найти периметр этой трапеции если его острый угол 60°​

Answer 1

Ответ:

Периметр трапеции равен 20 см

Объяснение:

Средняя линия равнобедренный трапеции равна 6 см. Диагональ образуется с большим основанием угол 30°. Найти периметр этой трапеции если его острый угол 60°.

ABCD - данная равнобедренная трапеция. BC||AD, AB=CD.

По условию задачи диагональ АС образует с большим основанием AD угол 30°: ∠CAD=30°. Углы при основании равнобедренной трапеции равны, и по условию составляют 60°: ∠A=∠D=60°.

Средняя линия трапеции равна 6 см.

РЕШЕНИЕ

1.

∠BAC=∠BAD-∠CAD=60°-30°=30°.

∠BCA=∠CAD=30° - как накрест лежащие углы, образованные при пересечении двух параллельных прямых BC и AD секущей AC.

∠BAC=∠CAD=30°.

Следовательно △ ABC - равнобедренный с основанием АС.

АВ=ВС - как боковые стороны равнобедренного треугольника.

Обозначим AB=BC=CD= x.

2.

Рассмотрим △ACD.

Так как сумма углов треугольника равна 180°, то ∠ACD=180°-∠CAD-∠D=180°-30°-60°=90°.

△ACD - прямоугольный.

Катет CD лежит напротив угла CAD=30°, а значит равен половине гипотенузы AD.

AD=2•CD=2x

3.

Так как средняя линия трапеции равна полусумме её оснований, то:

$\bf m = \dfrac{BC + AD}{2}$

$\sf \dfrac{x + 2x}{2} = 6$

3x=12

x=4.

Получили, что: АВ=ВС=CD=4(см); AD=2•4=8(см)

4.

Периметр трапеции равен сумме всех её сторон:

Р(ABCD)= AB+BC+CD+AD=4+4+4+8=20(см)

Ответ: 20 см

#SPJ1