Сократить дробь. (СРОЧНО, ЗАДАНИЕ НА ФОТО!!)
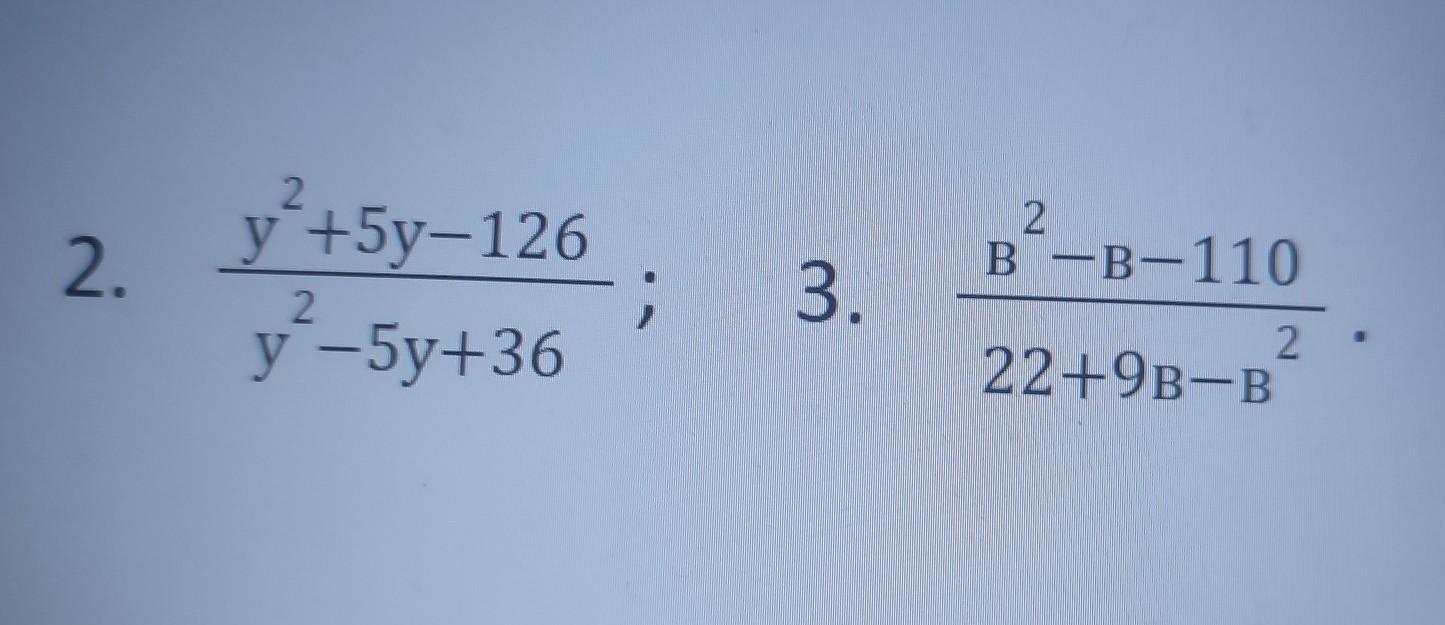
Ответы
Ответ:
Для сокращения дроби (2(y^2 + 5y - 126))/(y^2 - 5y + 36) можно разложить числитель и знаменатель на множители и сократить общие множители. В данном случае можно заметить, что числитель и знаменатель имеют общий множитель 2:
(2(y^2 + 5y - 126))/(y^2 - 5y + 36) = (2(y^2 + 5y - 126))/(y^2 - 5y + 36)
Теперь можно дальше упрощать числитель и знаменатель, если это возможно.
Для сокращения дроби (B^2 - B - 110)/(22 + 9B - B^2) можно также разложить числитель и знаменатель на множители и сократить общие множители. В данном случае можно заметить, что числитель и знаменатель имеют общий множитель B - 11:
(B^2 - B - 110)/(22 + 9B - B^2) = ((B - 11)(B + 10))/((B - 11)(-B - 22))
Здесь общий множитель (B - 11) сокращается, и окончательный результат будет:
((B - 11)(B + 10))/((B - 11)(-B - 22)) = (B + 10)/(-B - 22)