Question

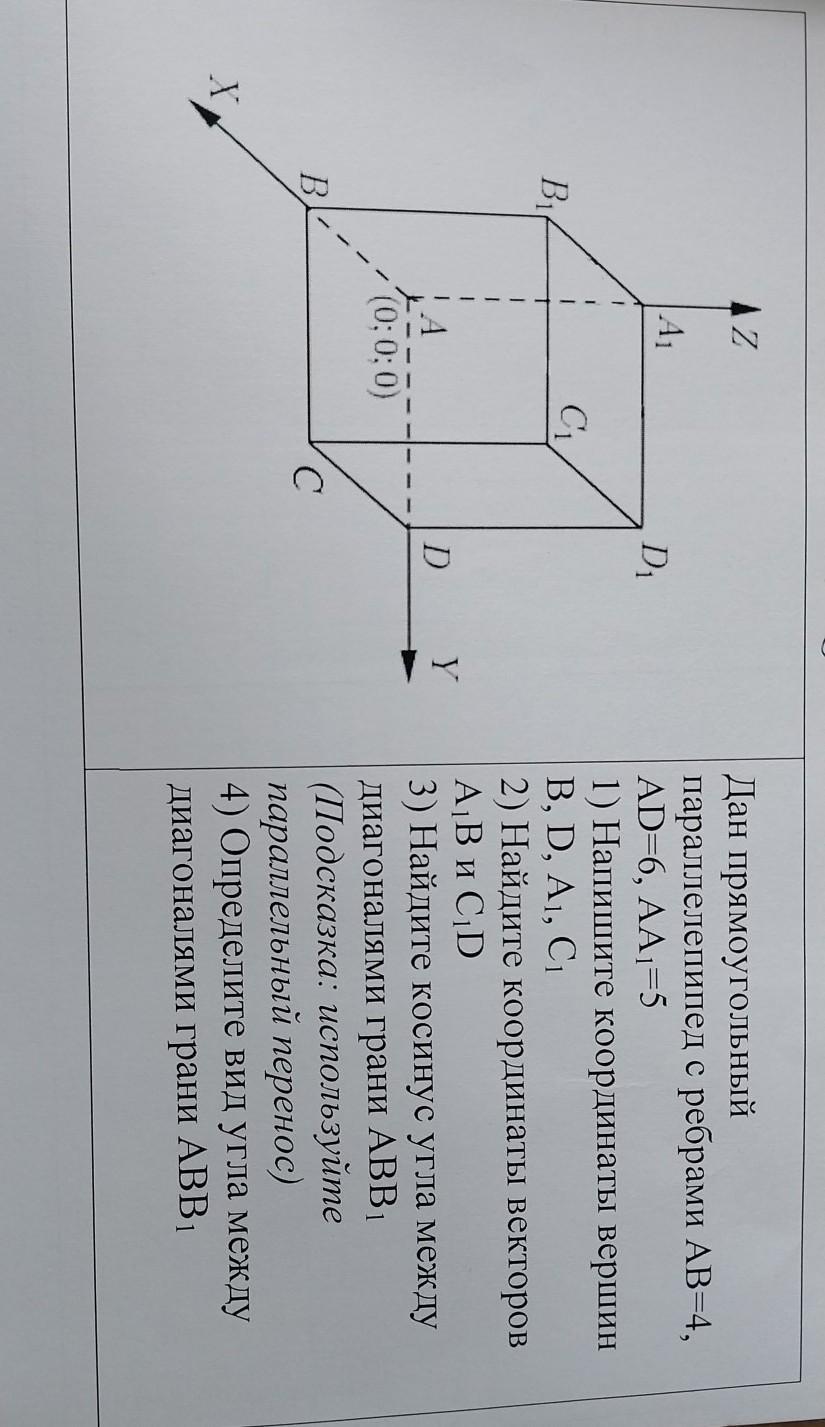
Дан прямоугольный параллелепипед с ребрами AB=4, AD=6, AA1=5 1) Напишите координаты вершин B, D, A1, Ci 2) Найдите координаты векторов A B и C D 3) Найдите косинус угла между диагоналями грани ABB (Подсказка: используйте параллельный перенос) 4) Определите вид угла между диагоналями грани ABB​

Answer 1

Ответ:

1) Координаты вершин:

A(0,0,0), B(4,0,0), C(4,6,0), D(0,6,0), A1(0,0,5), C1(4,6,5)

2) Координаты векторов:

AB = (4,0,0) - (0,0,0) = (4,0,0)

CD = (0,6,0) - (4,6,5) = (-4,-6,-5)

3) Диагонали грани ABB: AB и AC1. Параллельный перенос вектора AC1 на вектор AB даст вектор AD. Тогда косинус угла между диагоналями грани ABB равен косинусу угла между векторами AB и AD. Найдем длины векторов AB и AD:

|AB| = √(4^2 + 0^2 + 0^2) = 4

|AD| = √(4^2 + 6^2 + 5^2) = √77

AB · AD = 4·4 + 0·6 + 0·5 = 16

cos(AB, AC1) = AB · AD / (|AB| · |AD|) = 16 / (4·√77) = 2 / √77

4) Угол между диагоналями грани ABB является острым, так как косинус угла между ними положительный.