Предмет: Математика,
автор: Mikich0
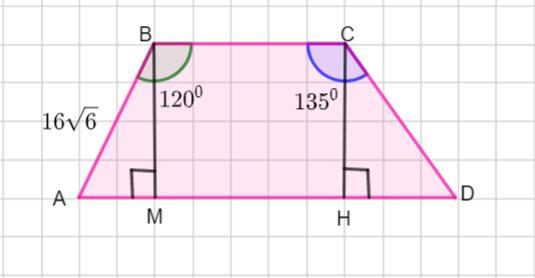
23. Найди длину боковой стороны CD трапеции ABCD, если углы BCD и ABC равны 135° и 120° соответственно, а АВ 16√6.
Приложения:

Annastasla:
Картинку не видно
Ответы
Автор ответа:
2
Ответ:
48 ед.
Пошаговое объяснение:
Найти длину боковой стороны CD трапеции ABCD, если углы BCD и АВС равны 135° и 120° соответственно , а АВ 16√6.
Пусть дана трапеция ABCD, ∠BCD = 135°, ∠ABC = 120°, АВ = 16√6.
Сумма углов при параллельных прямых ( односторонние углы) равна 180 ° . Тогда ∠ ВАD = 180 °- 120 ° = 60°, ∠АDС = 180° - 135°=45°.
Проведем высоты ВМ и СН .
Рассмотрим Δ АМВ - прямоугольный треугольник.
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
CH = BM = 24√2
Рассмотрим Δ СHD - прямоугольный
Значит , длина боковой стороны CD равна 48 ед.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Музыка,
автор: tresh1212
Предмет: Математика,
автор: ruslanashevchenko006
Предмет: Геометрия,
автор: someone5234
Предмет: Математика,
автор: Аноним
Предмет: История,
автор: polina655339