Question

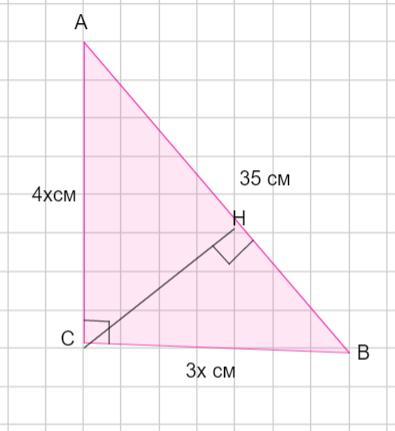
У прямокутному трикутнику гіпотенуза = 35 см , а катети відносяться як 3:4 . Знайдіть проекцію меншого катета на гіпотенузу

Answer 1

Ответ:

12,6 см

Объяснение:

В прямоугольном треугольнике гипотенуза 35 см, а катеты относятся как 3 : 4. Найти проекцию меньшего катета.

Пусть дан Δ АВС - прямоугольный ( ∠С =90°). Гипотенуза АВ =35 см.

ВС : АС = 3: 4 .

Пусть ВС = 3х см, а АС = 4х см.

Применим теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

АВ² =АС ² +ВС²;

АВ²= ( 4х)²+ (3х)²

Тогда получим уравнение

( 4х)²+ (3х)²  = 35²;

16х² +9х² = 1225:

25х² = 1225;

х² = 1225: 25;

х²= 49

Так как x>0, то х = √49 = 7  и  АС = 4· 7 = 28 см и ВС = 3 · 7 = 21 см.

Катет ВС - меньший. Надо найти проекцию этого катета на гипотенузу.

Проведем высоту СН  на гипотенузу АВ. Отрезок ВН - проекция катета ВС на гипотенузу.

Воспользуемся свойством: катет прямоугольного треугольника есть среднее геометрическое между гипотенузой и его проекцией на гипотенузу.

$BC = \sqrt{AB \cdot BH} ;\\\\21=\sqrt{35\cdot BH} ;\\\\21^{2} =35\cdot BH;\\\\BH =\dfrac{21^{2} }{35} =\dfrac{21\cdot 21}{35} =\dfrac{3\cdot 7\cdot 21}{7\cdot5} =\dfrac{63}{5} =\dfrac{63\cdot 2}{5\cdot 2} =\dfrac{126}{10} =12,6$

Тогда проекция катета ВС на гипотенузу равна 12,6 см.

#SPJ1