помогите, не понимаю
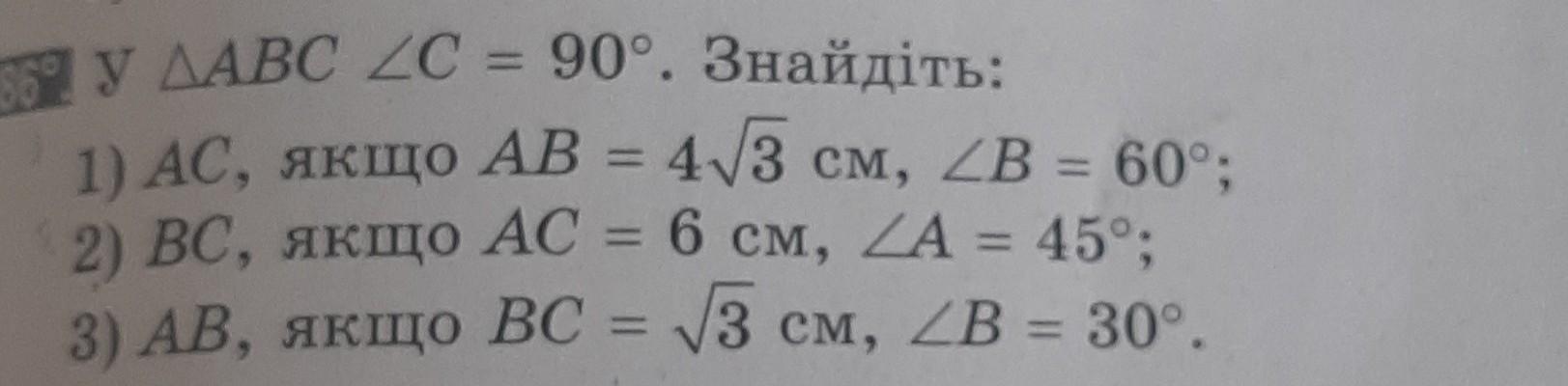
Ответы
Ответ:
Объяснение:
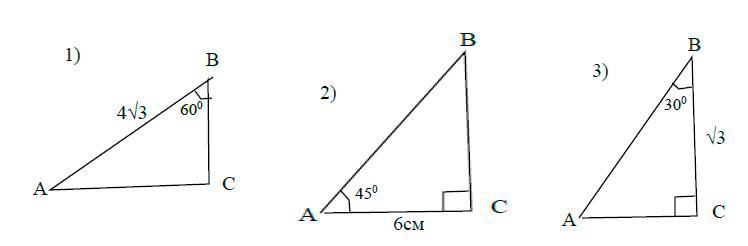
1) Дано:
ΔАВС
∠С = 90°
АВ =4√3(см)
противолежащего угла
__________
АС =? (см)
В прямоугольном Δ-ке катет равен гипотенузе, умноженный на синус противолежащего угла, т.е.
АС = АВ *sin∠B = AB*sin60° = 4√3 * √3/2 = 2*3 = 6(см)
АС = 6см
Можно решить и по т. Пифагора: квадрат гипотенузы = сумме квадратов катетов.
∠В = 90°, т.к. сумма всех угловΔ-ка = 180°, то ∠А = 180° -90° -60° = 30°
Против угла в 30° лежит катет, равный половине гипотенузы, т.е
ВС = АВ/2 = 4√3/2 = 2√3.
По теореме Пифагора:
АВ² = ВС² + АС², откуда
АС² = АВ² - ВС² = (4√3)² - (2√3)² = 16*3 - 4*3 = 3(16 - 4) = 3*12 = 36
АС = √36 = 6(см)
2)
АС = 6см
∠А = 45°
ВС - ? (см)
Т.к. ∠А = 45°, то и ∠В = 45° ( 180° - 90° -45° = 45°), т.е. углы при основании Δ-ка равны, следовательно, ΔАВС - равнобедренный:
АС = ВС = 6 (см)
3) ВС = √3
∠В = 30°
АВ - ?
В прямоугольном Δ-ке катет равен гипотенузе, умноженный на косинус угла, прилежащего к этому катету. Т.е.,
ВС = АВ*cos30° , откуда
АВ = ВС/cos30° = √3 /(√3/2) = 2
АВ =2(см)