Предмет: Геометрия,
автор: Аноним
A(2;1;4)
B(0;3;-1)
C(2;0;1)
Какие из них взаимно перпендикулярны
Тема: Скалярное произведение
Приложения:
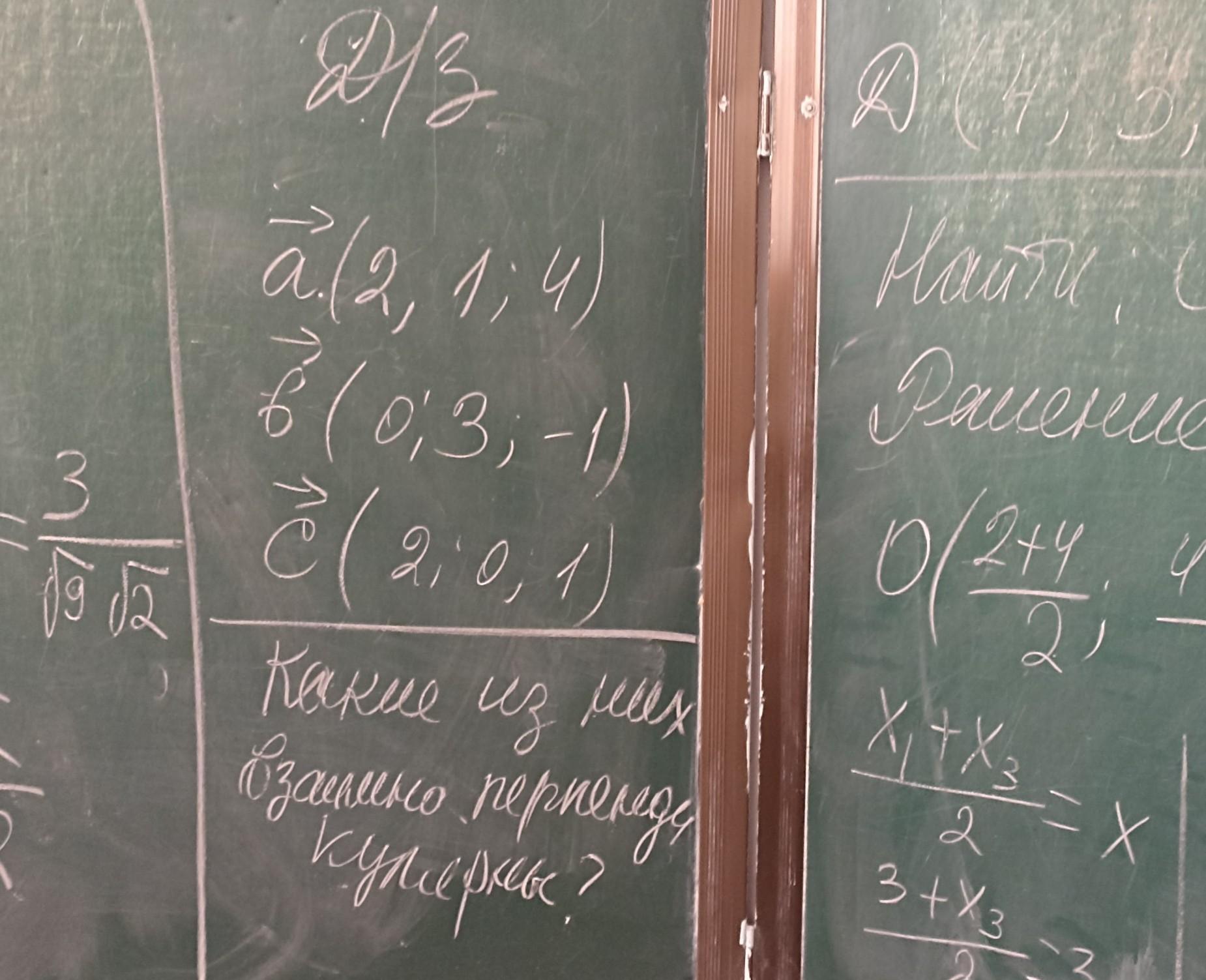
Ответы
Автор ответа:
1
Для того чтобы определить, являются ли данные векторы взаимно перпендикулярными, необходимо вычислить скалярное произведение каждой пары векторов и проверить, равно ли оно нулю.
Скалярное произведение двух векторов a и b вычисляется по формуле: a * b = |a| * |b| * cos(угол между векторами)
Таким образом, чтобы узнать, перпендикулярны ли векторы, нужно проверить, равно ли их скалярное произведение нулю.
Вычислим скалярное произведение каждой пары векторов:
AB = (0-2) + (9-3) + (-4+1) = -2 + 6 - 3 = 1
AC = (4-2) + (0-1) + (4-1) = 2 - 1 + 3 = 4
BC = (0-2) + (9-0) + (-4+1) = -2 + 9 - 3 = 4
Таким образом, скалярное произведение векторов AB и AC не равно нулю, а скалярное произведение векторов AB и BC, а также векторов AC и BC равно нулю. Следовательно, только векторы AB и BC являются взаимно перпендикулярными.
Скалярное произведение двух векторов a и b вычисляется по формуле: a * b = |a| * |b| * cos(угол между векторами)
Таким образом, чтобы узнать, перпендикулярны ли векторы, нужно проверить, равно ли их скалярное произведение нулю.
Вычислим скалярное произведение каждой пары векторов:
AB = (0-2) + (9-3) + (-4+1) = -2 + 6 - 3 = 1
AC = (4-2) + (0-1) + (4-1) = 2 - 1 + 3 = 4
BC = (0-2) + (9-0) + (-4+1) = -2 + 9 - 3 = 4
Таким образом, скалярное произведение векторов AB и AC не равно нулю, а скалярное произведение векторов AB и BC, а также векторов AC и BC равно нулю. Следовательно, только векторы AB и BC являются взаимно перпендикулярными.
Похожие вопросы
Предмет: Українська література,
автор: krutoi22832
Предмет: Литература,
автор: I1love2ylitki3
Предмет: География,
автор: Mizurakia
Предмет: Русский язык,
автор: charly07
Предмет: Алгебра,
автор: shamildaf