Предмет: Алгебра,
автор: Volodi512
Составьте уравнение плоскости
Прошу помогите!!!
Приложения:
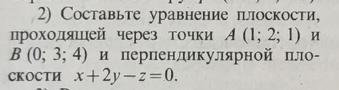
Ответы
Автор ответа:
2
Ответ:
Плоскость проходит через точки
перпендикулярно плоскости .
Нормальный вектор плоскости равен
Нормальный вектор искомой плоскости равен векторному
произведению .
Уравнение искомой плоскости имеет вид:
Похожие вопросы
Предмет: Русский язык,
автор: bagysbekovat
Предмет: Химия,
автор: saswws
Предмет: География,
автор: sashavosenko
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Ndusbk