Помогите срочно!
Напешыте на Укр языке
Ответы
Відповідь:
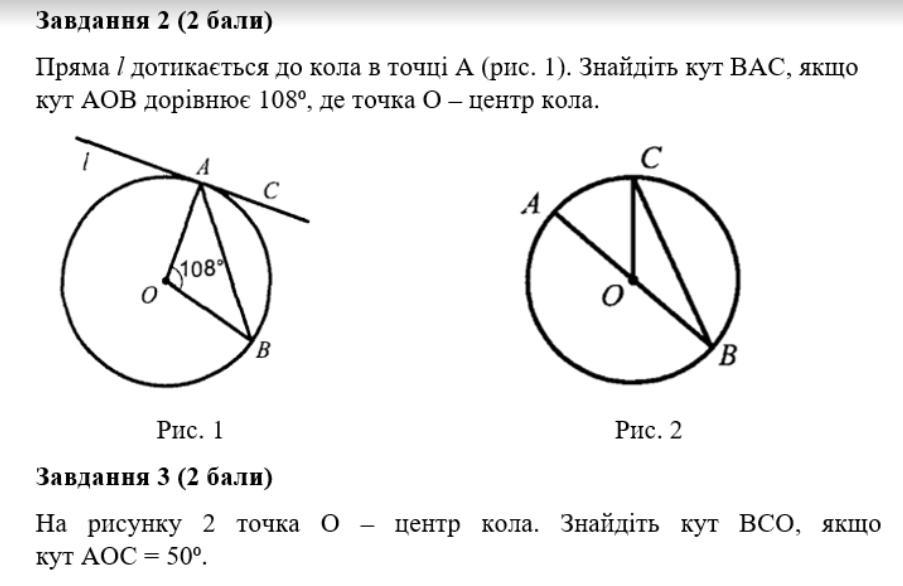
Завдання 1
Дано: коло з центром о, пряма1 - дотична, А - точка дотику, ∠АОВ = 108°.
Знайти: ∠ВАС.
Розв‘язання: радіус, проведений до точки дотику дотичної, перпендикулярний до цієї дотичної (ОА ⊥ АС).
ОА = ОВ як радіуси, тому трикутник АОВ - рівнобедрений.
Кути при основі рівнобедреного трикутника рівні, сума всіх кутів 180°.
Обчислюємо: ∠OAB = ∠OBA = (180° - ∠AOB) * 1/2 = (180° - 108°) * 1/2 = 36°
Оскільки ОА ⊥ АС, то ∠ОАС = 90°.
∠ВАС = ∠OAC - ∠OAB = 90° - 36° = 54°.
Відповідь: 54°.
Завдання 2
Дано: О - центр кола, ∠АОС = 50°.
Знайти: ∠ВСО.
Розв‘язання: трикутник СОВ рівнобедрений (ОС = ОВ як радіуси). Кути при основі рівнобедреного трикутника рівні, тому ∠ВСО = ∠СВО.
Зовнішній кут дорівнює сумі двох внутрішніх кутів не суміжних з ним.
За цією властивістю маємо ∠ВСО = ∠СВО = ∠АОС * 1/2 = 50° * 1/2 = 25°.
Відповідь: 25°.
Пояснення:
Повідомте якщо потрібні додаткові пояснення.