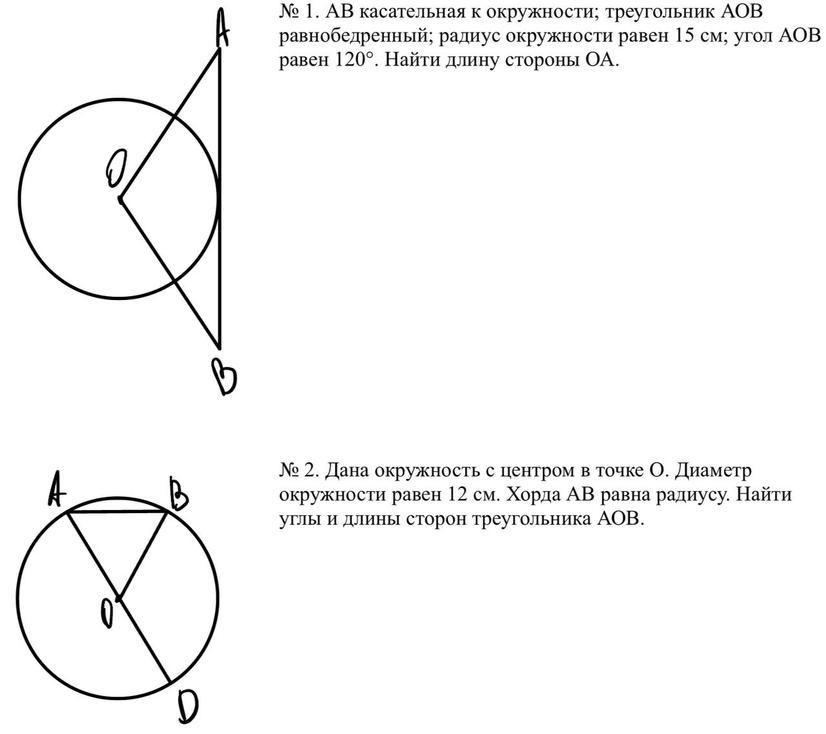
№ 1. AB касательная к окружности; треугольник АОВ
равнобедренный; радиус окружности равен 15 см; угол АОВ
равен 120°. Найти длину стороны ОА.
Ответы
Відповідь:
1)
Дано: АB - дотична, трикутник АОВ - рівнобедрений, r = 15 см, ∠АОВ = 120°.
Знайти: ОА.
Відповідь: додамо точку дотику К і проведемо до неї радіус ОК.
Радіус, проведений до точки до точки дотику дотичної перпендикулярний до цієї дотичної. Звідси маємо, що OK⊥AB. Оскільки ∠АКО = 90°, то ОК є висотою трикутника АОВ. У рівнобедренному трикутнику висота є також бісектрисою та медіаною.
Бісектриса ділить кут навпіл, тому ∠АОК = ∠АОВ * 1/2 = 60°.
Сума гострих кутів прямокутного трикутника 90°.
Обчислюємо: ∠ОАК = 90° - 60° = 30°.
Катет, що лежить напроти кута 30° дорівнює половині гіпотенузи.
ОК - катет, що лежить напроти кута 30°, а також радіус, тому ОК = 15 см. OA - гіпотенуза, тому маємо ОА = 2OK = 2*15 = 30см.
Відповідь: 30см.
2)
Дано: коло з центром О, d = 12см, хорда АB = r.
Знайти: ОА, АВ, ОВ, ∠А, ∠О, ∠В.
Розв‘язання: d = 2r. За цією формулою маємо, що ОА = АВ = ОВ = r = d * 1/2 = 12 * 1/2 = 6см.
трикутник АОВ рівносторонній (ОА = АВ = ОВ). Сума всіх кутів трикутника 180°. Обчислюємо:
∠А = ∠О = ∠В = 180° : 3 = 60°.
Відповідь: 60°, 60°, 60°, 6см, 6см, 6см.
Пояснення:
Додала додатково фото внизу.
