Предмет: Алгебра,
автор: Agent007Li
Довести тотожність:

Приложения:
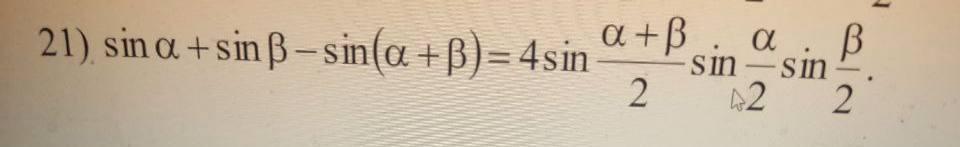
Ответы
Автор ответа:
1
Объяснение:
21)
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Українська література,
автор: sehdvi
Предмет: Українська мова,
автор: OblivionFire
Предмет: Английский язык,
автор: КаплинаКсения17