Предмет: Алгебра,
автор: veronikamila65
Помогите вычислить интеграл
Приложения:
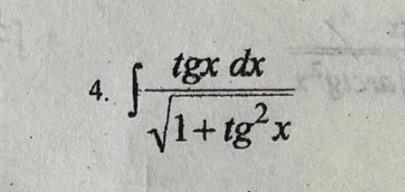
Ответы
Автор ответа:
1
Ответ:
(см. объяснение)
Объяснение:
Задание выполнено!
спасибо большое
а можно я добавлю еще один вопрос, интеграл, посмотрите ?пожалуйста
sgn(cos())*cos() = |cos()|
)))
)))
ответ соs(1+tg^2x ) что ли ?
Почему ответ был отмечен неверным? Вроде все преобразования законные, и он легче альтернативного?
Может быть ответ отмечен неверным, поскольку Вы его не упростили до |cos x|?
Кстати, если быть щепетильным, нужно разбивать первообразную на участки непрерывности, причем на каждом участке своя постоянная. Как в случае с \int dx/x= ln x+C_1, если x>0, и ln(-x)+C_2, если x<0.
Автор ответа:
1
Ответ:
Объяснение:
спасибо большое, очень подробно
а вы знаете метод симплекса ?
В студенческие годы приходилось использовать симплекс-метод, но как давно это было. Сейчас вряд ли возьмусь за такую задачу.
Похожие вопросы
Предмет: Українська література,
автор: n10249646
Предмет: Физика,
автор: alesya110684
Предмет: Информатика,
автор: Аноним
Предмет: Биология,
автор: nikitakaradzer64
Предмет: История,
автор: syzdykovagulim35
жалею что с вами связался