Предмет: Алгебра,
автор: pavelgorbach2408
СРОЧНО ПОМОГИТЕ ПОЖАЛУЙСТА
Приложения:
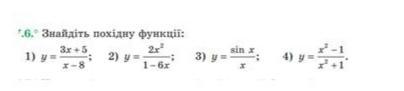
Ответы
Автор ответа:
2
1)
2)
3)
4)
pavelgorbach2408:
Не знаю твоего имени, но ты просто лучший-ая, помоги мне пожалуйста с остальными
Похожие вопросы
Предмет: Физика,
автор: mansur240711
Предмет: География,
автор: romashkaqqq
Предмет: Математика,
автор: kontarkarina
Предмет: Другие предметы,
автор: tuasayanyatm14
Предмет: Алгебра,
автор: looolyyman