Предмет: Математика,
автор: vladskydka89
Помогите срочно пожалуйста
Вычислить интеграл (метод замены переменной)
Приложения:
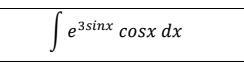
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Вычислить интеграл:
Замена переменной:
Получим интеграл:
Выполним обратную замену и получим ответ:
Похожие вопросы
Предмет: Английский язык,
автор: cureru
Предмет: География,
автор: foxcrazy019
Предмет: Литература,
автор: manabekovaajsa
Предмет: Алгебра,
автор: garanin062
Предмет: История,
автор: MaksMichurov