Question

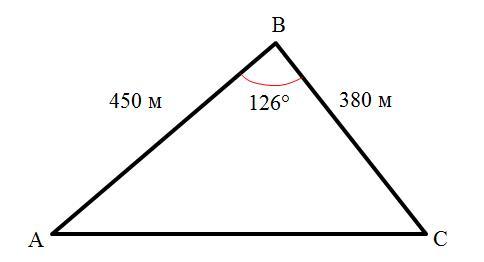
Длина стороны AB треугольника АВС равна 450 м, а длина ВС = 380 м. Угол между этими сторонами 1260. Вычислите периметр и площадь треугольника. Ответы округлить до сотых.

Answer 1

Ответ:

Периметр треугольника P(ABC) ≈ 1570,27 м

Площадь треугольника S(ABC) ≈ 69169,5 м²

Объяснение:

Нужно знать:

1) Площадь треугольника АВС можно вычислить по формуле:

$\tt \displaystyle S(ABC) = \frac{1}{2} \cdot AB \cdot BC \cdot sin \angle B,$

здесь AB и ВС стороны треугольника и ∠B - угол между этими сторонами.

2) Сторону AC треугольника АВС можно вычислить по теореме косинусов:

$\displaystyle \tt AC^2 = AB^2 + BC^2 - 2 \cdot AB \cdot BC \cdot cos \angle B,$

здесь AB и ВС стороны треугольника и ∠B - угол между этими сторонами.

3) Периметр треугольника АВС определяется через стороны треугольника по формуле:

P(ABC) = AB + BC + AC.

4) Формулы приведения:

sin(180°–α) = sinα; cos(180°–α) = –cosα.

5) Значения синуса и косинуса острых углов по таблице значений тригонометрических функций.

Решение. Известно: AB = 450 м, ВС = 380 м, ∠B = 126° (см. рисунок).

Вычислим площадь треугольника АВС (округляем до сотых):

$\tt \displaystyle S(ABC) = \frac{1}{2} \cdot 450 \cdot 380 \cdot sin 126^0=85500 \cdot sin(180^0-54^0)=85500 \cdot sin54^0=\\\\ \approx 85500 \cdot 0,809=69169,500 =69169,5 \; M^2.$

Находим сторону AC треугольника АВС по теореме косинусов (округляем до сотых):

$\displaystyle \tt AC^2 = 450^2 + 380^2 - 2 \cdot 450 \cdot 380 \cdot cos 126^0 =346900-342000 \cdot cos (180^0-54^0)=\\\\ =346900-342000 \cdot (-cos 54^0)\approx 346900+342000 \cdot 0,588 =\\\\=346900+201096=547996,000=547996, \\\\AC \approx 740,2675 \approx 740,27 \;M .$

Теперь вычислим периметр треугольника АВС:

P(ABC) = 450 + 380 + 740,27 = 1570,27 м.

#SPJ1