Question

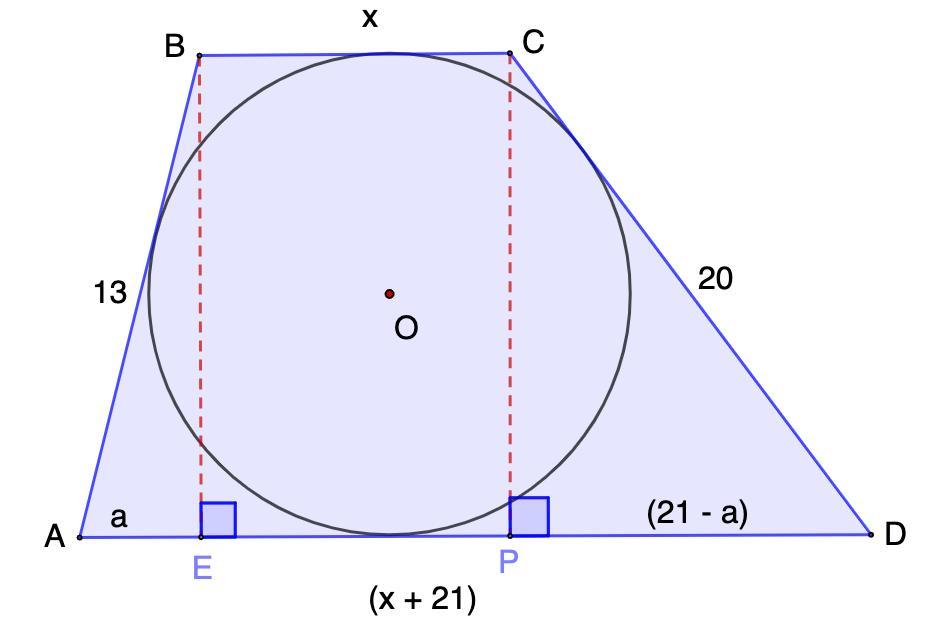
В четырехугольнике ABCD, описанном около окружности, АВ=13, CD=20, стороны AD и BC параллельны и AD-BC=21. Найдите площадь этого четырехугольника.

Answer 1

Ответ:

Площадь четырехугольника равна 198 ед².

Объяснение:

В четырехугольнике ABCD, описанном около окружности, АВ = 13, CD = 20,  стороны AD и BC параллельны и AD - BC = 21. Найдите площадь этого четырехугольника.

Дано: АВСD;

AD || BC;

Окр.О - вписана в АВСD;

АВ = 13, CD = 20; AD - BC = 21.

Найти: S(АВСD)

Решение:

Рассмотрим АВСD.

AD || BC   ⇒   АВСD - трапеция.

AD - BC = 21

Пусть ВС = х, тогда AD = х + 21

• Если в четырехугольник вписана окружность, то суммы противоположных сторон равны.

⇒ АВ + CD = BC + AD

13 + 20 = х + х + 21

2х = 12     |:2

х = 6

⇒ BC = 6; AD = 27.

Проведем высоты ВЕ и СР.

ЕВСР - прямоугольник.

• Противоположные стороны прямоугольника равны.

⇒ ВС = ЕР = 6

Тогда АЕ + РD = 21

Найдем высоту.

Рассмотрим ΔАВЕ и ΔРСD - прямоугольные.

Пусть АЕ = а, тогда PD = 21 - a

По теореме Пифагора:

Из ΔАВЕ:   ВЕ² = АВ² - АЕ²

Из ΔPCD:   CP² = CD² - PD²

BE = CP

⇒ АВ² - АЕ² = CD² - PD²

169 - a² = 400 - 441 + 42a - a²

42a = 210     |:42

a = 5

⇒ $BE = CP = \sqrt{169 - 25}=\sqrt{144}=12$

Найдем площадь трапеции ABCD.

• Площадь трапеции равна произведению полусуммы оснований на высоту.

$\displaystyle S(ABCD)=\frac{BC+AD}{2}\cdot BE=\frac{6+27}{2}\cdot12=198$

Площадь четырехугольника равна 198 ед².

#SPJ1