Предмет: Алгебра,
автор: 7386505
Знайдіть невизначені інтеграли, використовуючи виділення повного квадрата у знаменнику підінтегрального виразу
Приложения:
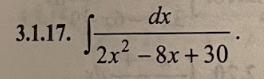
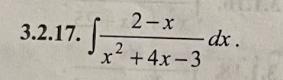
Ответы
Автор ответа:
1
Ответ:
1) Выделяем полный квадрат в знаменателе , получаем табличный интеграл.
2) Выделяем полный квадрат в знаменателе и разбиваем интеграл на два табличных .
veronikamila65:
добрый день, NNNLLL54 помогите пожалуйста решить интеграл, вы очень хорошо объясните, пожалуйста....
Похожие вопросы
Предмет: Литература,
автор: Аноним
Предмет: Английский язык,
автор: rimamanasan409
Предмет: Литература,
автор: k02783964
Предмет: История,
автор: Аноним