Радіус кола, вписаного в прямокутний трикутник дорівнює 3 см. Обчисліть периметр цього трикутника, якщо його гіпотенуза дорівнює 17 см.
СРОЧНО!!!
Ответы
Ответ:
Периметр трикутника дорівнює 40 см
Объяснение:
Радіус кола, вписаного в прямокутний трикутник дорівнює 3 см. Обчисліть периметр цього трикутника, якщо його гіпотенуза дорівнює 17 см.
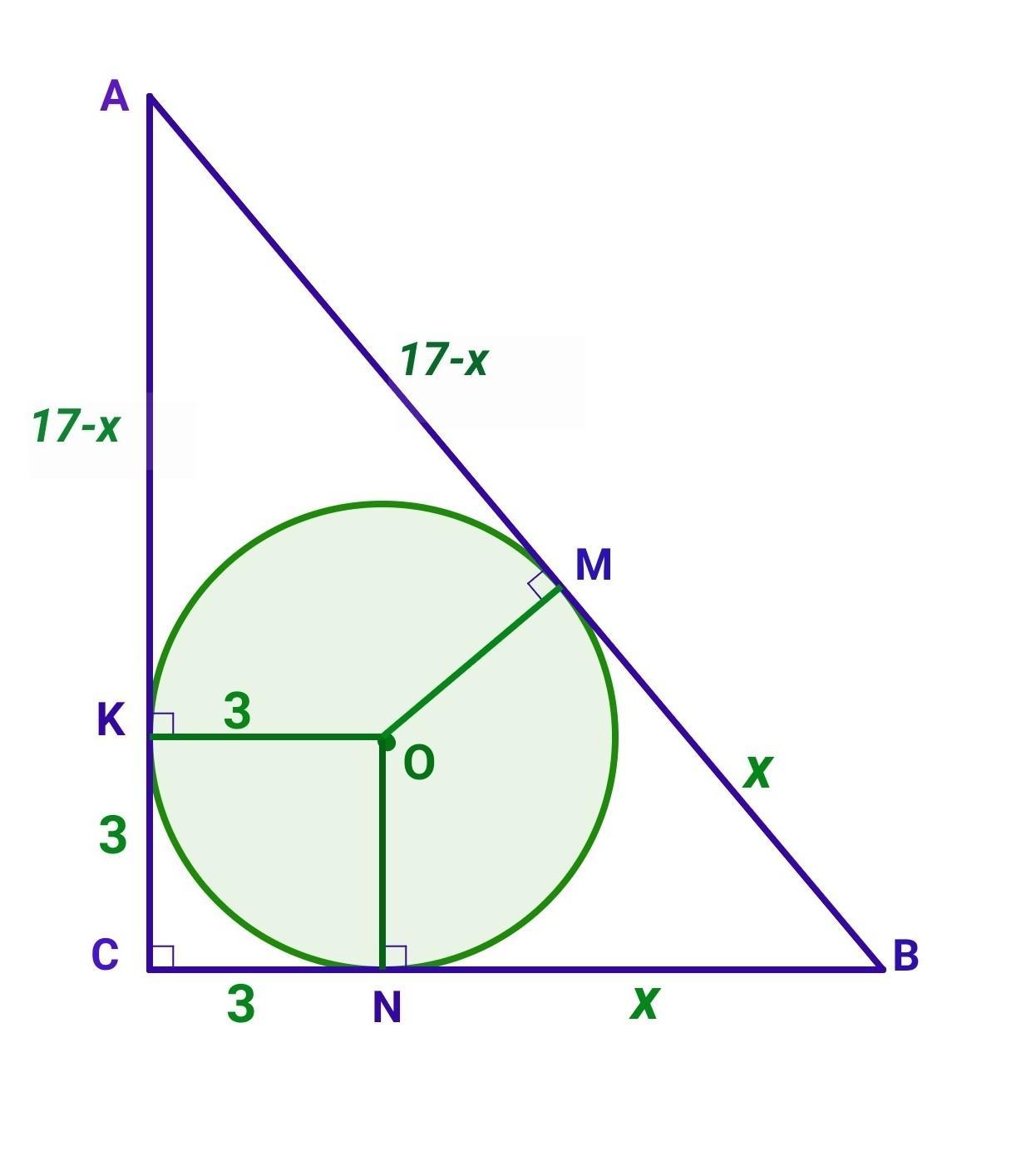
Нехай АВС - заданий прямокутний трикутник. ∠С=90°, r - радіус вписаного кола, r=3 см. Гіпотенуза АВ = 17 см.
Позначимо MB = х см, тоді АМ= (17-х) см.
Нехай точка О - центр вписаного кола, ОК, ОМ, ON - радіуси, проведені в точки дотику кола зі сторонами трикутника. Тоді OK⟂AC, ON⟂BC, ∠C=90°, тому KONC - прямокутник. Оскільки OK= ON=r, то KONC - квадрат. Тому:
OK=ON=KC=CN=r=3 см.
За властивістю дотичних до кола відрізки дотичних, проведених з однієї точки до точок дотику, рівні.
Тому:
AK=АM=(17-x) см,BM=BN=х (см).
За аксиомою вимірювання відрізків отримаємо:
AC=AK+KC=17-x+3=(20-x) см.
ВС=BN+CN=(x+3) см
З △АВС (∠С=90°) за теоремою Піфагора AB²=AC²+BC²
(20-х)²+(х+3)²=17²
400-40х+х²+х²+6х+9=289
2х²-34х+120=0
х²-17х+60=0
За теоремою Вієта отримаємо два корені: х₁=5; х₂=12
Тоді АС = 20-5= 15 (см), або АС=20-12=8 (см).
ВС=5+3=8 (см), або ВС = 12+3=15 (см)
Отже, катети прямокутного трикутника АВС дорівнюють 8 см і 15 см
Периметр трикутника ABC:
P=AB+BC+AC=17+8+15=40(см)
Відповідь: 40 см
#SPJ1