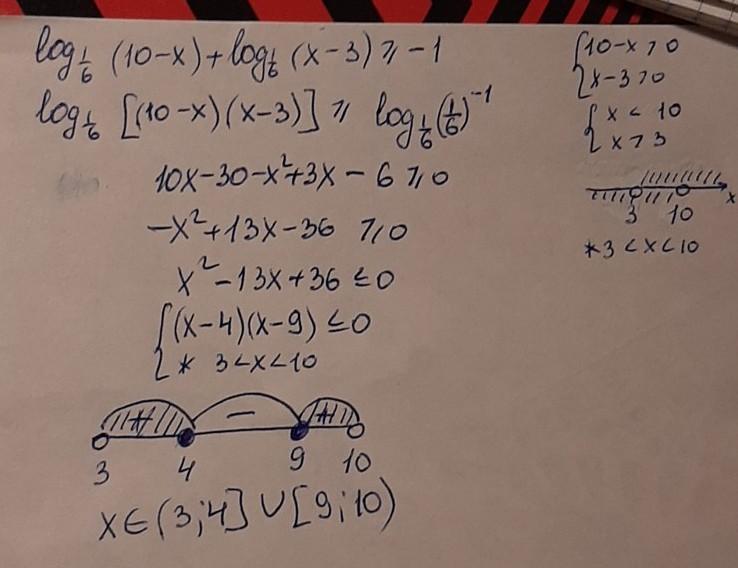Решить логарифмическое неравенство с рисунком
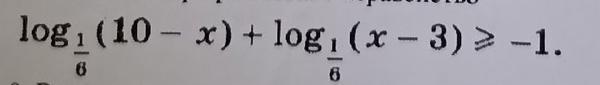
Ответы
Ответ:
Ответ: x ∈ (3;4] U [9;10)
Пошаговое объяснение:
Дано:
ОДЗ:
Применим свойство логарифмов
Так как , то
Теперь необходимо избавиться от в обеих частях неравенства, но перед этим проанализируем основание логарифма. Так как основание логарифма больше нуля и меньше единицы, то знак неравенства меняется на противоположный.
(10 - х)(х - 3) ≤ 6
-x² + 13x - 36 ≤ 0 | ·(-1)
x² - 13x + 36 ≥ 0
Нули функции y = x² - 13x + 36:
x² - 13x + 36 = 0
D = 25
Неравенство примет следующий вид:
(x - 4)(x - 9) ≥ 0
Решим неравенство с помощью метода интервалов.
------------------------------------●----------------------------------------●------------------->х
x ∈ (-∞;4] U [9;+∞)
Учитывая ОДЗ запишем ответ.
Ответ: x ∈ (3;4] U [9;10)
Решение логарифмического неравенства на фото