Предмет: Математика,
автор: danildanil0611
Решить логарифмическое уравнение с рисунком
Приложения:
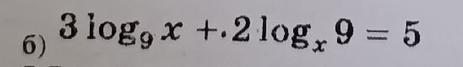
Ответы
Автор ответа:
2
Ответ:
x = 1;
Пошаговое объяснение:
Дано уравнение:
ОДЗ:
В общем-то нужно просто вспомнить одну прекрасную формулу
Тогда мы можем представить наше уравнение как:
Пусть
Нули числителя:
3t² - 5t + 2 = 0
D = 1
Произведем обратную замену:
∈ ОДЗ
x = 9 ∈ ОДЗ
danildanil0611:
Спасибо за решение, сможете решить ещё уравнений?
рад был помочь, попозже может смогу
У меня в профиле пару уравнений, если будет время решите пожалуйста, до завтрашнего утра(8:00)
Автор ответа:
2
Решеник логарифмического уравнения на фото
Приложения:
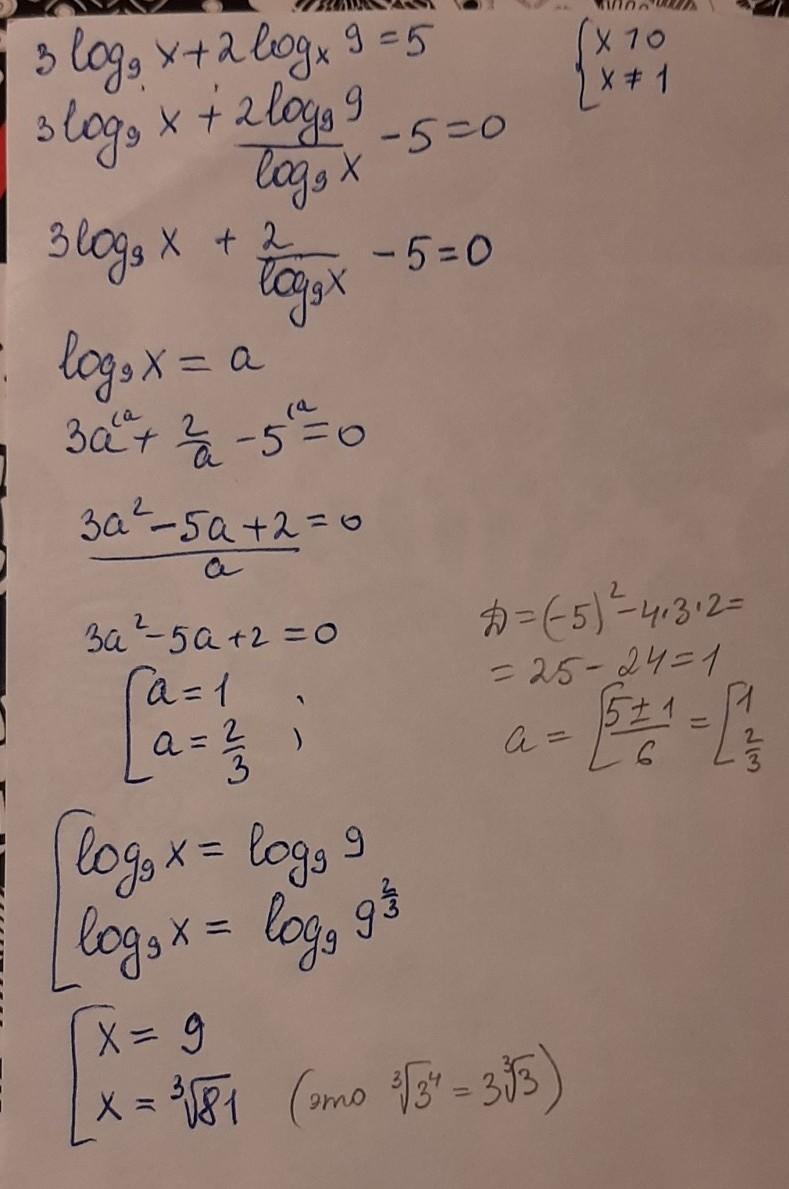
Похожие вопросы
Предмет: Українська мова,
автор: putatinskaai
Предмет: Литература,
автор: illiabardachenko142
Предмет: Химия,
автор: mihajloandraska
Предмет: Литература,
автор: mimimishkahse