Question

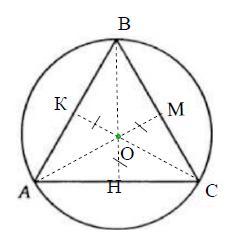
Усі сторони трикутника. вписаного в коло, розташовані на однаковій відстані від центра кола. Доведіть, що цей трикутник рівносторонній.

Answer 1

Ответ:

Объяснение:

Дано:
ΔАВС
ОК = ОН = ОМ
т.О - центр описанной окружности.
____________
Док. ,что ΔАВС - равносторонний

Центр окружности, описанной около треугольника, — это точка пересечения серединных перпендикуляров его сторон, т.е.
1) ОК ⊥ АВ и АК =КВ
  ОН ⊥ АС и АН = НС
  ОМ ⊥ ВС и ВМ = МС

2) Рассмотрим ΔНОС и ΔМОС. Эти Δ-ки прямоугольные и
ΔНОС = МОС по гипотенузе и катету (два прямоугольных Δ-ка равны если гипотенуза и катет одного треугольника равны гипотенузе и катету другого треугольника:  ОН =ОМ по условию, ОС = общая сторона). Значит, и
НС = МС, но НС = АН, А МС = ВМ, следовательно,
НС = АН = МС =МВ  → НС + АН = МС + МВ или
АС = ВС

3) Аналогично для ΔКАО и ΔНОА:
ΔКАО =  ΔНОА по гипотенузе (АО) и катету (КО =НО). Значит,
АН =АК или
АН = НС = АК = КВ
АН+НС = АК + КВ
АС = АВ
Т.к. АС = ВС, то
АС = АВ = ВС, т.е. ΔАВС - равносторонний, ч.т.д.