Предмет: Геометрия,
автор: kkata1402
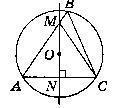
551.° Через центр О кола, описаного навколо трикутни- ка ABC, проведено пряму, яка перпендикулярна до сторони АС і перетинає сторону AB у точці М. Доведіть, що АМ = MC.
Приложения:

Ответы
Автор ответа:
2
Відповідь:
Дано:
Коло з центром О описане навколо трикутника ABC. О є l, l ┴ АС, l ∩ АВ = М.
Довести: AM = МС.
Доведения:
Центр кола, описаного навколо трикутника, знаходиться в точці перетину
серединних перпендикулярів.
Якщо через центр кола проведена пряма l, яка перпендикулярна сторонi АС,
тоді N - точка перетину прямої l i сторони АС, буде серединою сторони AC
i тоді MN - медіана.
Якщо MN - висота i медіана, тоді ∆АМС - рівнобедрений, AM = МС.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: max796181
Предмет: Оʻzbek tili,
автор: dilnurmuminovna
Предмет: Музыка,
автор: wldkssmxnsmsk
Предмет: Математика,
автор: al6670519
Предмет: Қазақ тiлi,
автор: horshilovaolesya05