Question

Очень срочно, помогите пожалуйста
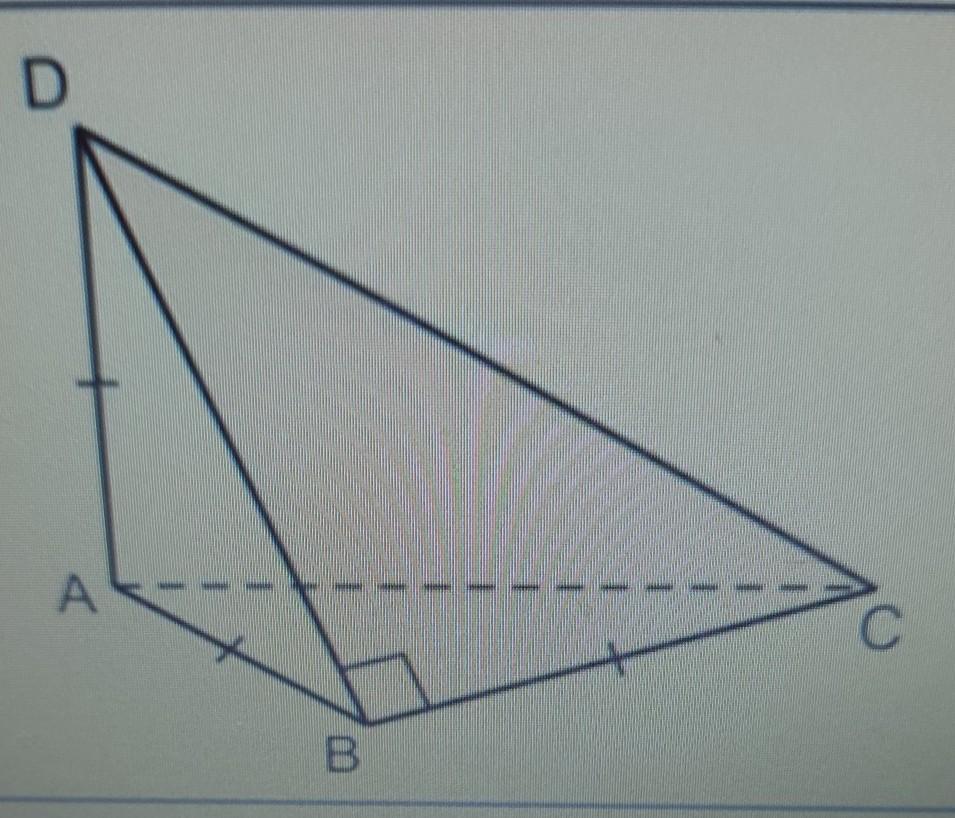
Треугольник ABC - основание пирамида DABC, угол DBC равен 90°, DA - высота пирамиды, AD=AB=BC. Площадь боковой поверхности пирамиды равна 18+36√2. Найдите высоту пирамиды. ​

Answer 1

Ответ:

DA=6ед

Объяснение:

АВ=ВС=АD=x.

В прямоугольном равнобедренном треугольнике, по теореме Пифагора гипотенуза будет

√(х²+х²)=√(2х²)=х√2

S(∆DAB)=½*DA*AB=x*x/2=x²/2

S(∆DBC)=½*DB*BC=x*x√2/2=x²√2/2

S(∆DAC)=½*DA*AC=x*x√2/2=x²√2/2

Sбок=S(∆DAB)+S(∆DBC)+S(∆DAC)=

=x²/2+x²√2/2+x²√2/2=(x²+2x²√2)/2

Sбок=18+36√2

Уравнение:

(х²+2х²√2)/2=18+36√2. |×2

х²+2х²√2=36+72√2

х²(1+2√2)=36+72√2

х²=(36+72√2)/(1+2√2)

х²=(36(1+2√2))/(1+2√2)

х²=36

х=6 ед высота